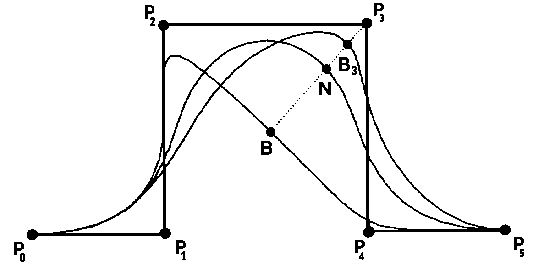
Fig. 2: Geometric meaning of weights (w_3).
sum(i = 0, n){w_i * P_i * N_i,k(u)}
C(u) = -------------------------------------, (1)
sum(i = 0, n){w_i * N_i,k(u)}
where
w_i : weights P_i : control points (vector) N_i,k : normalized B-spline basis functions of degree k
These B-splines are defined recursively as:
u - t_i N_i,k(u) = ----------- * N_i,k-1(u) + t_i+k - t_i t_i+k+1 - u --------------- * N_i+1,k-1(u) (2) t_i+k+1 - t_i+1and
/ 1, if t_i <= u < t_i+1
N_i,0(u) = <
\ 0, else
where t_i are the knots forming a knot vector
U = { t_0, t_1, ... , t_m }.
The sequence of knots in the knot vector U is assumed to be nondecreasing, i.e. t_i <= t_i+1. Each successive pair of knots represents an interval [t_i, t_i+1) for the parameter values to calculate a segment of a shape [FOLEY][WATT].
For NURBS, the relative parametric intervals (knot spans) need not be the same for all shape segments, i.e. the knot spacing is nonuniform, leading to a non-periodic knot vector of the form
U = { a, ... , a, t_k+1, ... , t_m-k-1, b, ... , b }, (3)
where a and b are repeated with multiplicity of k+1 [ROGERS][PIEGL]. The multiplicity of a knot affects the parametric continuity at this knot [FOLEY]. Non-periodic B-splines, like NURBS, are infinitely continuously differentiable in the interior of a knot span and k-M-1 times continuously differentiable at a knot, where M is the multiplicity of the knot [ROGERS]. (In contrast, a periodic knot vector U = { 0, 1, ... , n } is everywhere k-1 times continuously differentiable.) Considering the knot vector for NURBS, the end knot points (t_k, t_n+1) with multiplicity k+1 coincide with the end control points P_0, P_n.
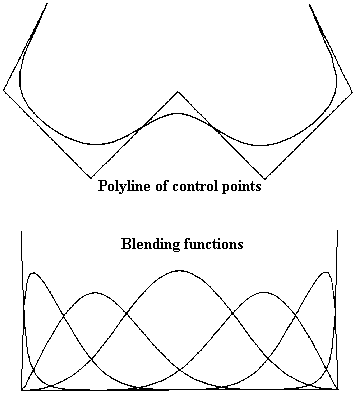
Since the knot spacing could be nonuniform, the B-splines are no longer the same for each interval [t_i, t_i+1) and the degree of the B-Spline can vary [WATT][FOLEY]. Considering the whole range of parameter values represented by the knot vector, the different B-splines build up continuous (overlapping) blending functions N_i,k(u), as defined in (2), over this range (Fig. 1) [WATT]. These blending functions have the following properties: [WATT][ROGERS]
w_i * N_i,k(u)
R_i,k(u) = ----------------------------
sum(j = 0, n){w_j * N_j,k(u)}
into
C(u) = sum(i = 0, n){P_i * R_i,k(u)}.
A NURBS-surface is define in a similar way:
S(u, v) = sum(i = 0, n)sum(j = 0, m) P_i,j * R_i,k, j,l(u, v) ,
where
w_i,j * N_i,k(u) * N_j,l(v)
R_i,k,j,l(u, v) = ---------------------------------------------------------
sum(r = 0, n){sum(s = 0, m){w_r,s * N_r,k(u) * N_s,l(u)}}
The rational basis functions have the same properties as the blending functions [PEIGL][ROGERS]. One point to emphasize, is their invariance under affine and (even) perspective transformations. Therefore, only the control points have to be transformed to get the appropriate transformation of the NURBS shape.
C'(u) = sum(i = 0, n){P_i'(u) * N_i,k(u)}
/ ( X1/W, X2/W, ... , Xn/W ), if W not = 0
map( X1, X2, ... ,Xn, W) = <
\ ( X1, X2, ... , Xn ), if W = 0
sum(i = 0, n){w_i * P_i * N_i,k(u)}
C(u) = map( C'(u) ) = -----------------------------------
sum(i = 0, n){w_i * N_i,k(u)}
For u in [t_i, t_i+1), the only existing blending functions to consider in evaluation of the curve at u are N_i-k,k(u), ..., N_i,k(u). An effective algorithm for the computation of the non-vanishing blending functions exists in [deBOOR pp. 132 - 135].
Defining the points:
B = C(u; w_i = 0)
N = C(u; w_i = 1)
B_i = C(u; w_i not = {0, 1})

Fig. 2: Geometric meaning of weights (w_3).
N and B_i can also be expressed as:
N = (1 - a) * B + a * P_i B_i = (1 - b) * B + b * P_i ,where
a = R_i,k(u; w_i = 1) b = R_i,k(u).
The following identity is obtained from the expression of a and b:
(1 - a)/a : (1 - b)/b = P_iN/BN : P_iB_i/BB_i = w_i ,
which is called the cross- or double ratio of the four points P_i, B, N, B_i. From these expressions, the effect of shape modification can be derived:
Markus Altmann / madwpi@cs.wpi.edu