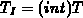
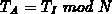
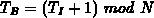
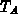 ) and noise(
) and noise(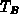 )
)
Dr. Matthew O. Ward
Computer Science Department
WPI
Random Numbers in Graphics
Just Call random()
Fields of Random Noise
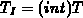
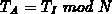
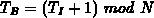
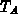 ) and noise(
) and noise(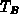 )
)
Linear Interpolation
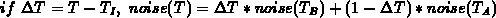
This gives smooth transitions between nodes, but only 0th order continuity at nodes.
Easy to extend to arbitrary dimensions.
Polynomial Fits are Better
Here is an example of a random field using Catmull-Rom splines for
interpolation.

Noise is Good, Turbulence is Better
We can impose self-similarity on noise to add scale-invariance. The turbulence at a point is created by summing the noise at that point with scaled down noise values at other points.
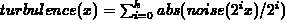
where k is the smallest integer for which 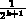 is greater
than the size of a pixel in real coordinates.
This is very similar to fractal surface generation, giving a visual
impression of brownian motion.
is greater
than the size of a pixel in real coordinates.
This is very similar to fractal surface generation, giving a visual
impression of brownian motion.
Here is an example of a turbulent field using the random field as a basis.
I show it using grey scale and a random color map.


Using Turbulence
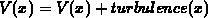
or 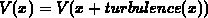
Applications
Marble Texture: Add turbulence to sine wave, use a curve through color space instead of a ramp
Here is an example of a sine wave with added turbulence.
I show it using grey scale and a random color map.


Tree Bark: Add turbulence to a sawtooth wave and use to bump map surface
Stars: Intensity of points based on distance to the center. Add
turbulence to this distance.
Here is an example of a star with added turbulence.

Flames: Compute intensity of point based on distance from center in x.
Scale it based on distance in y. Add turbulence. Use 3-D turbulence to
animate.
Here is an example of a flame with added turbulence.

Conclusions