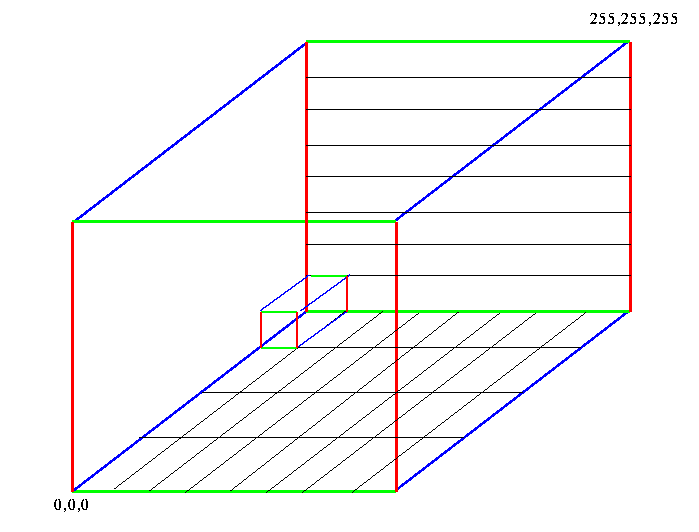
Uniform Quantization
In uniform quantization each axis of the color space is treated
independently. Each axis is then divided into equal sized
segments. The planes perpendicular to the axis' that pass through the
division points then define regions in the color space. The number of
these regions is dependent on the scheme used for dividing the color
space. One possible scheme is to divide the red and green axis into 8
segments each and the blue axis into 4 resulting in 256
regions. Another possibility is dividing the red and blue into 6 and
the green into 7 segments resulting in 252 regions [3]. Each one of these regions will produce a color for the color map.
Once the color space has been divided each of the original colors
is then mapped to the region which it falls in. The representative
colors for each region is then the average of all the colors mapped to
that region. Because each of the regions represents an entry in the
color map, the same process for mapping the original colors to a
region can be repeated for mapping the original colors to colors in
the color map. While this algorithm is quick and easy to implement it
does not yield very good results. Often region in the color space will
not have any colors mapped to them resulting in color map entries to
be wasted.
This algorithm can also be applied in a non-uniform manner if the axis
are broken on a logarithmic scale instead of linear. This will produce
slightly better results because the human eye cannot distinguish dark
colors as well as bright ones.
