Median Cut Algorithms
The premise behind median cut algorithms is to have every entry in the
color map represent the same number of pixels in the original image.
In contrast to uniform sub-division, these algorithms divide the color
space based on the distribution of the original colors. The process is
as follows[2]:
- Find the smallest box which contains all the colors in the
image.
- Sort the enclosed colors along the longest axis of the box.
- Split the box into 2 regions at median of the sorted list.
- Repeat the above process until the original color space
has been divided into 256 regions.
The algorithm then divides the color space in a manner depicted below.
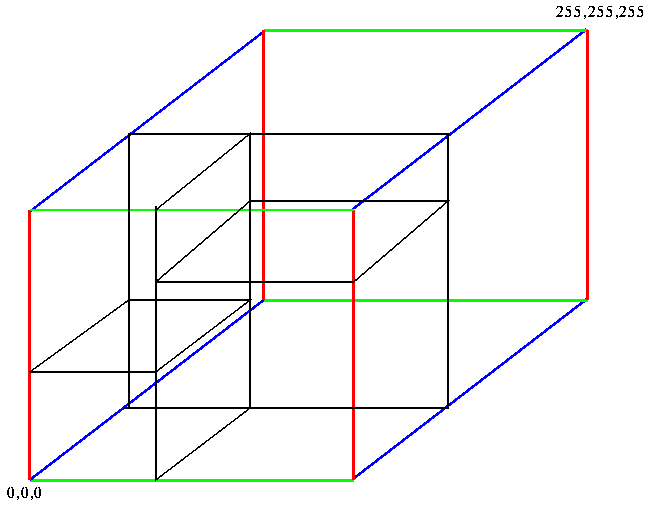The representative colors are found by averaging the colors in each
box, and the appropriate color map index assigned to each color in
that box.
Because these algorithms use image information in dividing the color
space this class of algorithms consistently produce good results while
having memory and time complexity no worse than popularity
algorithms[1]