Aliasing - Point Sampling Theory

The key points are as follows:

Point sampling in the spatial domain corresponds to the point by point multiplication of a sampling impulse function times the analog signal to be sampled.
The Fourier Transform of an impulse function with spacing T in the spatial domain results in an impulse function with spacing 1/T in the frequency domain
The multiplication of two functions in one domain coresponds to the convolution of the Fourier Transforms of the two functions in the other domain
The convolution of an impulse function with another function is the second function instanciated at the impulse function positions.

Look at examples of point sampling without and with aliasing:

In the time domain: The top signal is sampled at the Nyquist limit and so is not aliased but the bottom signal is sampled at a rate below the Nyquist limit and is aliased.

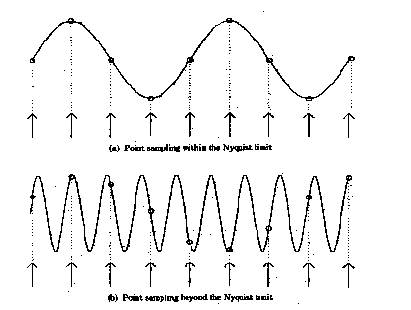
In the frequency domain: The left side corresponds to the top in the above image and the right side corresponds to the lower signal. Note that, for the left side case, after the reconstruction filter is applied, we obtain a signal identical to the initial signal, i.e., no aliasing has occurred. In the right side case, there is an overlap between the input signal instanciations and after the reconstruction filter is applied we do not have the original signal, but instead we now have two frequencies, both of which are lower than the original. This is aliasing.

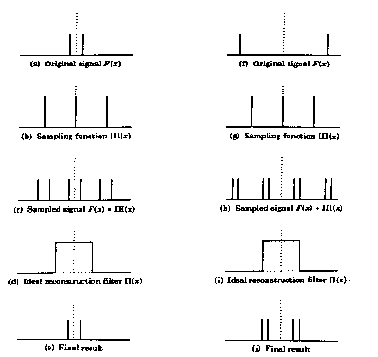
Note that the ideal reconstruction filter is a box in the frequency domain. This corresponds to a sinc filter (sin (x) / x) in the spatial domain. The sinc function is infinite, which means that it is impossible to have a perfect reconstruction filter in the spatial domain.

Back to the main screen