Final Project: Playing Solitaire

Before you tackle the homework, remind yourself of our General Advice, Advice on Homeworks, and Grading Guidelines. Above all, keep your work neat and honest.

Due Date: December 8, 1999

Background Solitaire is a board game for individuals. The board comes in various shapes. Here is the simplest one:

	      o     
	     o o    
	    o x o  
	   o o o o                         

The red x represents an unoccupied hole; the os are little pegs sticking in holes; and = stands for the surrounding wood.

The goal of the game is to eliminate the pegs one by one until only one peg is left. A player can eliminate a peg if it one of the neighboring holes is unoccupied and if there is a peg in the hole in the opposite direction. In that case, the second peg can jump over the first one and the first one is eliminated.

For example, on the above board, no peg can be eliminated. But, if the initial hole is on the side like this:

	      o
	     o o
            o o x
	   o o o o

then the blue and the cyan peg could jump. If the player decides to move the blue one, the next configuration is

	      x
	     o x
            o o o
	   o o o o

Problem: Develop a program that solves a Solitaire problem for different sizes of the equilateral triangle. You may choose to specify the input as the number of rows, e.g., 4, or as a list of lists of symbols, e.g.,

    '((o = = =)           = <=> WOOD 
      (o x = =)           o <=> PEG
      (o o o =)           x <=> HOLE
      (o o o o))

You must specify your choice.

The hole should always be placed at the right-most position in the second row. (If you care, you may wish to modify this choice for your own curiosity.)

The function solitaire should return false, if the given problem is not solvable. Otherwise, it should produce a list of moves that specifies in what order the pegs must be moved to solve the given Solitaire problem. Again, you must choose a representation for moves. Structures are a good choice.

Design Review: Your team must have a design review with a labby by Sunday, December 5. For the design review, you must turn in

1. data definitions for the board and moves on the board
   you may wish to specify moves in terms of pairs of indices
2. a translation of the above examples of boards into your chosen data representations
3. a contract, header, purpose statement for solitaire
4. an adjective that characterizes the kind of design recipe you want to use for solitaire
5. a Scheme definition of solitaire plus headers, contracts, and purpose statements for all of the auxiliary functions mentioned in the definition.
If you do not review your design with a labby by the deadline, you will get NO credit for your project.

Product: You must turn in the following:

1. the signed and dated paper copy of your design review
2. the program with
   1. a contract and purpose for each definition
   2. a block comment with tests
   3. (optional) any other intermediate material you used to develop the individual procedures

Sample Solution: One sample solution (something that resembles what you should turn in) is around 240 lines long. With an additional 70 lines, the developer of this assignment produced a graphical user interface that allows the user to pick the initial hole and shows the solution on-screen (based on draw-lib.ss): The YELLOW peg is the one that jumps over the BLACK into the BLUE hole.

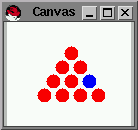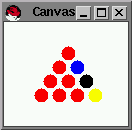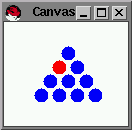There is a clever solution that is just under 190l lines.

Challenge: Modify the program so that it solves Solitaire for a different shape, e.g.,

      = = o o o = =
      = = o o o = =
      o o o o o o o
      o o o x o o o
      o o o o o o o
      = = o o o = =
      = = o o o = =

This problem is also well-known and more difficult than the triangle version.

You should modify your program so it computes two variants of the solution. In the first, pegs can jump in all possible directions: vertical, horizontal, and diagonal. In the second, pegs can jump only in the vertical and horizontal direction. The difference consists of five lines of code.

Warning: A straightforward adaptation of the triangle-shape program requires around four hours on a 166Mz, Linux laptop for the first problem, and an overnight run for the second one.

The challenge carries no credit.