4.0 Introduction

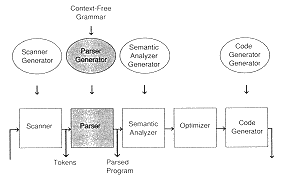
A parser generator, also called a syntax analyzer generator, follows the form shown in Chapter 1:

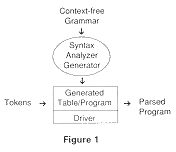
Although syntax analysis is more powerful than lexical analysis (a parser can recognize tokens), it is not necessarily more complicated to generate one. In fact, generation of a top-down parser is relatively simple.

Generation

The metalanguage for a parser generator is a context-free grammar. This context-free grammar is usually expressed in Backus-Naur form, BNF, or extended Backus-Naur form, EBNF, themselves metalanguages for context-free grammars. EBNF differs from BNF, allowing shortcuts resulting in fewer but more complicated productions. In this text, we often say the metalanguage for a parser generator is BNF.

The BNF in Example 1 is more complicated than that shown in Chapter 1 because top-down parser generation places more restrictions on the grammar.

Example 1 shows the parser generator converting this BNF into tables (or a Case statement). The form of the tables depends upon whether the generated parser is a top-down parser or bottom-up parser. Top-down parsers are easy to generate; bottom-up parsers are more difficult to generate.

4.1.1 Metalanguage Restriction

The grammar from Modules 1 and 2 actually has two problems which a top-down parser generator must eliminate. We discuss these as preprocessor steps to the parser generator.

Left-Recursion

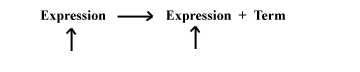
The grammar for assignment statements from Modules 1 and 2 is left-recursive; that is, in the process of expanding the first nonterminal, that nonterminal is generated again:

The most reasonable top-down parsing method is one where we look only at the next token in the input. Looking at more than the next token has proved too time-consuming in practice.

Parsing, here initiated by the driver program, proceeds by expanding productions until a terminal (token) is finally generated. Then that terminal is read from the input and the procedure continues. If the first nonterminal is the same as that being expanded, as in the production for an expression above, it will be continually and indefinitely expanded without ever generating a terminal that can be matched in the grammar.

Generation of top-down parsers may require a preprocessing step that eliminates left-recursion.

Common Prefix

A second problem is caused by two productions for the same nonterminal whose right-hand side begins with the same symbol:

S --> a

S --> a

These two productions contain a common prefix, and once again the parser, as initiated by the driver looking at only the next symbol in the input, does not know which of these productions to choose. Fortunately, grammars can be changed to eliminate these problems. We will show algorithms for changing the grammars to eliminate both left-recursion and common prefixes.

4.1.2 Elimination of Left-Recursion

There is a formal technique for eliminating left-recursion from productions

Step One: Direct-Recursion

For each rule which contains a left-recursive option,

A --> A |

introduce a new nonterminal A' and rewrite the rule as

A --> A'
A' --> | A'

Thus the production:

E --> E + T | T

is left-recursive with "E" playing the role of "A","+ T" playing the role of , and "T" playing the role of A'. Introducing the new nonterminal E', the production can be replaced by:

E --> T E'
E' --> | + T E'

Of course, there may be more than one left-recursive part on the right-hand side. The general rule is to replace:

A --> A | | ... | | | ... |

by

A --> A' | A'| ...| A'
A' --> | A' | A' | ...| A'

Note that this may change the "structure". For the expression above, the original grammar is left-associative, while the non-left recursive one is now right-associative.

Step Two: Indirect-Recursion

Step one describes a rule to eliminate direct left recursion from a production. To eliminate left-recursion from an entire grammar may be more difficult because of indirect left-recursion. For example,

A --> B x y | x

B --> C D

C --> A | c

D --> d

is indirectly recursive because

A ==> B x y ==> C D x y ==> A D x y.

That is, A ==> ... ==> A where is D x y.

The algorithm eliminates left-recursion entirely. It contains a "call" to a procedure which eliminates direct left-recursion (as described in step one).

Example 3 illustrates this algorithm for the grammar of Example 3.

4.1.3 Elimination of Common Prefixes

The procedure to eliminate a common prefix is called left-factoring.

The formal technique is quite easy. Simply change:

A --> | | ... |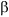

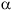
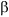
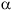
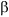
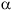
to

A --> 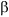A'

A' --> | | ... |

4.2 LL(1) Parser Driver

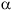
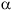
Top-down parsing proceeds by expanding productions, beginning with the start symbol. The grammar must be LL(1)

In order to define LL(1), we need two preliminary definitions: FIRST and FOLLOW. FIRST is defined for a sentential form; FOLLOW is defined for a nonterminal.

FIRST(), for any sentential form , is the set of terminals that occur left-most on any string derivable from including if is derivable from .

For a nonterminal A in a sentential form, say A where and are some string of terminals and nonterminals,

FOLLOW(A) = FIRST()

That is, FOLLOW(A) is the set of terminals that can appear to the right of A in a sentential form.

A grammar is LL(1) if and only if given any two productions A , A ,

(a) FIRST () FIRST( ) = , and

(b) If one of or derives ,

• ...

  then FIRST()FOLLOW(A) = .

  Elimination of left-recursion and left-factoring aid in producing an LL(1)grammar. If the grammar is LL(1), we need only examine the next token to decide which production to use. The magic table contains a production at the entry for Table[Nonterminal, Input Token].

  Top-down parsing uses a stack of symbols, initialized to the start symbol.

  Algorithm

  LL(1) Parser Driver

                     Push a $ on the stack.
                     Initialize the stack to the start symbol. 
                    REPEAT WHILE stack is nonempty:
                               CASE top of the stack is: 
          terminal:   IF input symbol matches terminal, THEN 
                           advance input and pop stack, ELSE error     
   nonterminal:   Use nonterminal and current input symbol to find correct production in table. 
                       Pop stack  
                     Push right-hand side of production  from table onto stack, last symbol                       first. 
                    END REPEAT
                     If input is finished, THEN accept, ELSE error

  Example 4 shows this algorithm in action with the grammar from Example 1 and the input string a := b * c + d ;

  4.3 Generating LL(1) Parsing Tables

  Constructing LL(1) parsing tables is relatively easy (compared to constructing the tables for lexical analysis). The table is constructed using the following algorithm:

  Algorithm

  LL(1) Table Generation

  For every production A in the grammar:

  1. If can derive a string starting with a (i.e., for all a in FIRST( ) ,

  Table [A, a] = A

  2. If can derive the empty string, , then, for all b that can follow a string derived from A (i.e., for all b in FOLLOW (A) ,

  Table [A,b] = A

  Undefined entries are set to error, and, if any entry is defined more than once, then the grammar is not LL(1).

  EXAMPLE 5 Constructing an LL(1) parse table entry using rule 1

  Consider the production E TE' from the non-left-recursive, left-factored expression grammar in Example 4. FIRST(TE') = { (, Id }, so Table[E,(] = E TE' and Table[E,Id] = E TE'.

  ---

  EXAMPLE 6 Constructing an LL(1) parse table entry using rule 2

  Consider the production E' from the same grammar of Example 4. Since ";", ")" and "$" are in FOLLOW (E'), this production occurs in the table in the row labeled E', and under the columns labeled ";", ")", and "$".

  ---

  LL(1) parsing tables may be generated automatically by writing procedures for FIRST () and FOLLOW(A). Then, when the grammar is input, A and are identified for each production and the two steps above followed to create the table.

  4.4 Recursive Descent Parsing

  LL(1) parsing is often called "table-driven recursive descent". Recursive descent parsing uses recursive procedures to model the parse tree to be constructed. For each nonterminal in the grammar, a procedure, which parses a nonterminal, is constructed. Each of these procedures may read input, match terminal symbols or call other procedures to read input and match terminals in the right-hand side of a production.

  Consider the Assignment Statement Grammar from Example 1:

       Program --> Statements     Statements --> Statement Statements'     Statements' -->  | Statements     Statement --> AsstStmt ;     AsstStmt --> Id = Expression     Expression --> Term Expression '     Expression' --> + Term Expression'                     |       Term     --> Factor Term'     Term'   --> * Factor Term'                 |      Factor --> (Expression)            | Id           | Lit

  In recursive descent parsing, the grammar is thought of as a program with each production as a (recursive) procedure. Thus, there would be a procedure corresponding to the nonterminal Program. It would process the right-hand side of the production. Since the right-hand side of the production is itself a nonterminal, the body of the procedure corresponding to Program will consist of a call to the procedure corresponding to Statements. Roughly, the procedures are as follows:

          Procedure Program        BEGIN { Program }                Call Statements     {Statements}                PRINT ("Program found")        END { P }

  The procedure corresponding to Statements also consists of calls corresponding to the nonterminals on the right-hand side of the production:

          Procedure Statements        BEGIN { Statements }                Call Statement                 Call Statements'                 PRINT ("Statements found")        END { Statements }

  Skipping to the procedure corresponding to AsstStatement:

          Procedure AsstStatement        BEGIN { AsstStatement }                If NextToken = "Id" THEN                        BEGIN                        PRINT ( " Id found " )                        Advance past it                        If NextToken = " =  " THEN                                BEGIN  { IF }                                        PRINT  (" = found")                                        Advance past it                                        Call E                                END  { IF }                        END                PRINT  ( "AsstStatement found" )        END  { AsstStatement }

  Procedures Expression and Expression' would be:

          Procedure  Expression        BEGIN  { Expression }                Call  Term                Call  Expression'                PRINT ("Expression found")        End  { Expression }    
  Procedure Expression'          BEGIN { Expression' }         IF NextSymbol in input = " + "         THEN BEGIN { IF } PRINT ( "+ found" )          Advance past it          Call   Term          Call    Expression    PRINT ("Expression' found") END { IF } END { Expression' } 
      
  This procedure works fine for correct programs since it presumes that if    "+" is not found, then the production is E'  . . 
      
  Procedures Term and Term' are similar since the grammar productions for them are    similar. Procedure Factor could be written: 
      
          Procedure Factor        BEGIN { Factor }        CASE NextSymbol is"(" :   PRINT ( "( found " )        Advance past it        Call Expression        If NextSymbol =")" THEN        BEGIN { IF }                PRINT ( " ) found")                Advance past it                PRINT ( "Factor found")        END { IF }        ELSE                error"Id":           PRINT ("Id found")                Advance past it                PRINT (" Factor found ")Otherwise:      error        END { Factor }
      
  Here, NextSymbol is the token produced by the lexical analyzer. To    advance past it, a call to get the next token might be made. The PRINT statements will    print out the reverse of a left derivation and then the parse tree can be drawn by hand or    a procedure can be written to stack up the information and print it out as a real    left-most derivation, indenting to make the levels of the "tree" clearer. 
      
  Recursive descent parsing has the same restrictions as the general LL(1) parsing method    described earlier. Recursive descent parsing is the method of choice when the language is    LL(1), when there is no tool available, and when a quick compiler is needed. Turbo Pascal    is a recursive descent parser. 
  
  4.5 Error Handling    in LL (1)Parsing
      
  Much work has been done in error handling for parser generators. Some    perform a recovery process so that parsing may continue; a few try to repair    the error. Topdown parsers detect the erroneous token when it is shifted onto the    stack. An error report might be 
      
        
  Unexpected erroneous token
      
      
  with the parser driver attempting a recovery based upon the choices that would have    been valid instead of the errorneous token. The attempted recovery, adding or deleting    tokens, may be made to either the stack or the input. Error handling similar to that used    for recursive descent parsing is described in Lemone (1992). The method was developed by    Niklaus Wirth in 1976. It requires that a set of firsts and followers be    maintained or computed for each production. 
   
   
  4.6 Summary 
      
  This chapter discusses top-down parser generators. 
      
  Given a grammar which is LL(1), it is easy to use an LL(1) parser generator. It is even    easy to write an LL(1) parser generator. 
      
  If the underlying language is LL(1), but the grammar is not , that is, it contains    left-recursion or common prefixes, then the grammar must be changed, a fairly complicated    process. 
      
  If the underlying language is not LL(1), however, bottom-up parsing techniques may need    to be used.