
2.0 Introduction
A scanner generator, also called a lexical analyzer generator, looks like this:

In Figure 1, the scanner is shown in two parts - the table or program stub which is generated and the driver which is written, not generated.
2.1 Metalanguage
The metalanguage for a scanner generator is a set of regular expressions describing the tokens in the language. A program stub or finite state table is generated from the regular expressions. At compile-time, the driver reads input characters from the source program, consults the table based upon the input and the current state, and moves to a new state based upon the entry, perhaps prforming an action such as entering an identifier into a name table.
We will illustrate these concepts with a sample language consisting of assignment statements whose right-hand sides are arithmetic expressions.
Example 1

We see that Identifiers are defined to consist of a sequence of one or more letters and digits beginning with a letter and that a literal consists of a sequence of digits. The allowable operators are those for addition, subtraction, multiplication, division and assignment.
These regular expressions are input to the generator to produce state tables either in table form or as a case statement program stub.
These regular expressions are input to the generator to produce state tables either in table form or as a case statement program stub.
Example 2
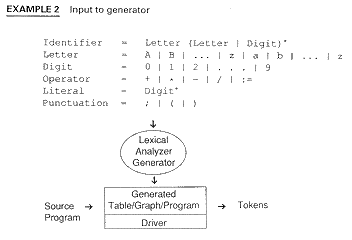
In Section 2.2 and in Section 2.3, we discuss the two programs, the driver program and the lexical analyzer generator.
2.2 The Driver
In this section, we will presume the table has been created by magic. Rows in the table represent states, columns are input characters, and the entries in the table are states.
The lexical analyzer (the driver) considers the input source program as a long sequence of characters with two pointers: a current and a lookahead pointer:

When lexical analysis begins to find
the next token, current and lookahead both point to the same
character: 
In the algorithm, four actions are performed on these pointers:
Algorithm
Driver for Lexical Analysis
WHILE there is more input
InputChar := GetChar
State := Table[0,
InputChar]
WHILE State != Blank
InputChar := GetChar
State := Table[State, InputChar]
ENDWHILE
Retract
Accept
Return token = (Class, Value)
ENDWHILE
- GetChar: Moves the lookahead pointer ahead one character and returns that character.

- Retract: Moves the lookahead pointer back one character.
Before Retract

After Retract

- Accept: Moves the current pointer ahead to the lookahead pointer:
After Accept

- Return: Returns a token consisting of a class and a value, as well as performs any actions associated with that state, e.g., installing an identifier into the name table.
The driver program scans the input program and comsults the entry at Table[State, InputChar] for the new state. The entry at Table[State, InputChar] consists of a new state and perhaps an action to be performed before moving to the new state:
In the algorithm retract is necessary when a token is found because the algorithm will have scanned one character too far.
Example 3

The magically created table
When the driver algorithm begins, the current and lookahead pointers are initialized to the character preceding the input. (See Exercise 2 )

The first input character, the X, is input (read by GetChar),
and the next state is at Table [0, Letter] (See Exercise 3) .
The entry
there is state 1. The input looks like:

Since state
entry is not blank, the algorithm enters the inner WHILE loop, and GetChar returns
a new InputChar, the "1":

The driver
continues and computes a new state, the entry at Table[1, digit,]
which is also a "1". Thus on encountering a digit, the lexical
analyzer stays in state 1. Returning to the condition in the inner WHILE, the
algorithm computes that the state is still not blank; this GetChar returns
the next character, either a space or, if all spaces have been removed, (See Exercise 2 )
the ";".

There is no
entry at Table[1, space] or Table[1,:], so the condition in the inner WHILE
fails and the algorithm executes the statements outside the inner WHILE, first
performing a retract operation:

Then, the accept
operation is performed, moving the current pointer ahead to the lookahead
pointer:

The token returned
is that associated with state 1, probably a token with class equal to Id,
and a value equal to the characters in the identifier or an index into a name
table where the identifier is installed (See Exercise 3 )
The lexical
analyzer driver now continues with the outer WHILE loop until input is
exhausted.
Example 2.3
shows a piece of a state table and the execution of the algorithm on an input
string. Rows represent states, columns are input characters, and the entries in
the table are states.
2.3 The Generator
Section 2.2
asks the reader to assume that the table is built by magic. The truth is that
translating regular expressions to a state table or case statement is more
tedium than magic. In this section, we will outline the steps and leave the algorithm
to the reader (see Exercises 7 to 9 ).
Lexical
Analyzer Generator Step 0: Recognizing a Regular Expression
A regular
expression is either:
- empty (null) , representing no strings
at all, denoted by

 denoting the language consisting of
the empty string
denoting the language consisting of
the empty string  (Sometimes
(Sometimes
 is
used to denote the empty string and the associated regular expression.)
is
used to denote the empty string and the associated regular expression.) - a single letter e.g., a representing
the language consisting of an a.
- the union of two regular expressions a
and b, denoted by a | b (also sometimes denoted by
a + b or a U b )
- the concatenation of two regular
expressions a and b, denoted by a
 b
(often the
b
(often the  is omitted").
is omitted"). - the Kleene closure. which is the union
of
 with a, with a
with a, with a  a,
with a
a,
with a  a
a  a,
etc. and denoted a*.
a,
etc. and denoted a*.
a* = {![]() } U
a U a
} U
a U a ![]() a U a
a U a ![]() a
a ![]() a U ...
a U ...
To convert
a regular expression to a finite automaton requires the recognition of ![]() ,
|, * and
,
|, * and ![]() as well as the individual characters in the sets.
Recognition of
as well as the individual characters in the sets.
Recognition of ![]() is not really possible, so the resulting
automaton will have to be converted to one which has no
is not really possible, so the resulting
automaton will have to be converted to one which has no
![]() -
transitions.
-
transitions.
2.2.1 Lexical Analyzer
Generator Step 1:
Converting a Regular Expression to a Finite
Automaton
There are
six steps (a) - (f):

The
diagram above shows that the regular expression e is recognized by a nondeterministic finite
automaton that has no way to get to a final state.

The
diagram above shows that the regular expression ![]() is recognized by the nondeterministic
finite automaton which goes from its initial state to its final state by
reading no input. Such a move is called an
is recognized by the nondeterministic
finite automaton which goes from its initial state to its final state by
reading no input. Such a move is called an ![]() - transition
- transition
In table
form this would be denoted:

The reader
may be wondering about an input of ![]() and how it would be
recognized by the driver. In fact, it will not be. This is just a first step in
table creation, and we will allow the creation of a nondeterministic finite
automation (NFA). Section 2.2.2 outlines how to turn this NFA into a
deterministic finite automation (DFA)
and how it would be
recognized by the driver. In fact, it will not be. This is just a first step in
table creation, and we will allow the creation of a nondeterministic finite
automation (NFA). Section 2.2.2 outlines how to turn this NFA into a
deterministic finite automation (DFA)

The
diagram above shows that the language {a} denoted by the regular expression a
is recognized by the finite automatation that goes from its initial to
final state by reading an a. In table from this would be:


In the
diagram above, we presume that the languages denoted by the regular expressions
R![]() and R
and R![]() , respectively, are recognized by the finite
automata denoted by M
, respectively, are recognized by the finite
automata denoted by M![]() and M
and M![]() .
.
Adding ![]() -transitions
to the beginning and end creates a finite automation which will recognize
either the language represented by R
-transitions
to the beginning and end creates a finite automation which will recognize
either the language represented by R or the language
represented by R
![]() , i.e., the union of these two languages, LR
, i.e., the union of these two languages, LR![]() U LR
U LR![]() .
.
We could
eliminate the new final state and the ![]() -transitions to it by letting
the final states of M
-transitions to it by letting
the final states of M![]() and M
and M![]() remain final states.
remain final states.
In table
form, this is:

Here, the
table entry for f is shown in a different row because the process of
recognizing strings in either LR![]() or LR
or LR![]() may lead to other intermediate
states.
may lead to other intermediate
states.
Our
example, which recognizes
Letters = A | B | C | . . . | a | b | . . . |z
and
Literal = 0 | 1 | 2 | . . . | 9
will use
this step.

In the
diagram above, M![]() is the machine that accepts LR
is the machine that accepts LR![]() and M
and M![]() is
the language that accepts LR
is
the language that accepts LR![]() . Thus, after this combined automation has
recognized a legal string in LR
. Thus, after this combined automation has
recognized a legal string in LR![]() , it will start looking for legal strings LR
, it will start looking for legal strings LR![]() .
This is exactly the set of strings denoted by R
.
This is exactly the set of strings denoted by R![]()
![]() R
R![]() . The related table
is:
. The related table
is:

Here the
table leads from an initial state, i, to the final state of M![]() upon
recognition of strings in LR
upon
recognition of strings in LR![]() , then from the final state in M
, then from the final state in M![]() , fM
, fM![]() to
the initial state in M
to
the initial state in M![]() on an
on an ![]() -transition, that is, without
reading any input, and then from the initial state in M
-transition, that is, without
reading any input, and then from the initial state in M![]() , iM
, iM![]() to the final
state in M
to the final
state in M![]() , fM
, fM![]() upon recognizing the strings
in LR
upon recognizing the strings
in LR![]() . The
. The ![]() is often omitted. It is
understood that two regular expressions appearing next to one another
represents the concatenation. We will use this step for the example, when we
define an identifier as a string of letters and digits (concatenated). Another
example will recognize a literal as the concatenation of one or more digits,
that is,
is often omitted. It is
understood that two regular expressions appearing next to one another
represents the concatenation. We will use this step for the example, when we
define an identifier as a string of letters and digits (concatenated). Another
example will recognize a literal as the concatenation of one or more digits,
that is,
Identifier = Letter (Letter | Digit)*
means
Identifier = Letter (letter | Digit)*

Here, M is
a finite automation recognizing some LR. A new initial state is added leading
to both M and to a new final state. The ![]() - transition recognizes the
empty string,
- transition recognizes the
empty string, ![]() (if R
did not contain
(if R
did not contain ![]() already).
The transition to M causes the language LR to be recognized. The
already).
The transition to M causes the language LR to be recognized. The ![]() transition from all final states of R to its
initial state will allow the recognition of LR
transition from all final states of R to its
initial state will allow the recognition of LR![]() , i = 1, 2,... The table is:
, i = 1, 2,... The table is:

We will
use this step as well as the preceding two, for the regular expressions
Identifier = Letter (Letter | Digit)*
and
Literal = Digit* = Digit Digit*
Using
these diagrams as guidelines, we can "build" a nondeterministic
finite automation from any regular expression (See Exercise 6 )
2.2.2 Lexical Analyzer
Generator Step 2:
Converting from an NFA to a DFA
As we saw
in

In Figure
2, one can go from state 1 to either state 1 or state 2 upon reading a
"$".
These two
possibilities, ![]() -transitions and multiple transitions on the
same input, represent nondeterminism.
-transitions and multiple transitions on the
same input, represent nondeterminism.
To convert
from an NFA to a DFA, we eliminate these two possibilities by grouping states
in the NFA. A state in the DFA will consist of a group (set) of states from the
NFA.
The new
start state is the same as the old start state.
With the
new start state we group all the states we can get to upon reading the same
input in the NFA; this process is continued with all the states of the NFA that
are in any set of states in the DFA.
Any state
in the DFA that contains a final state of the NFA is a final state.
For the
NFA above, the new start state is 0', the prime to distinguish it from the old
start state. State 1' = {1} since the only state accessible from state 0 in the
NFA is state 1:

The
situation is different for transitions from 1'={1}. Upon reading a letter or a
digit, the transition is back to state 1. We can add that transition to the
DFA:

But there
are two transitions upon reading "$" in the NFA, a move to state 1
and a move to state 2. We group these states into a new state called 2'={1, 2}
in the DFA.
The DFA
now is:

The state
2'={1,2} contains the old final state 2, so it is a final state.
If we are
in state 2', so it is a final state. If we are in state2' = {1, 2} and the
input is a letter or a digit, there is a transition back to 1' (because there
is a transition from 1 to 1 in the NFA). Finally, there is a transition from 2'
to 2' in the DFA upon reading a $ ( because there is a transition from 1 to 1
upon reading a $ in the NFA and 2'={1, 2}). The final DFA is:

This step
of the lexical analyzer generator, conversion of a regular expression to a DFA,
has shown the automata in the state-transition form. This could equally well
have been shown in table form (See Exercise 7).
The step
for removing ![]() -transitions is similar; all the states
accessible via an
-transitions is similar; all the states
accessible via an ![]() -transition are grouped (See Exercise 6).
This step can frequently result in DFA's with many states, some of which are
performing the same function and can be combined. This is a necessary step in
generating a lexical analyzer since there may be hundreds of states in the
table for the tokens in a programming language.
-transition are grouped (See Exercise 6).
This step can frequently result in DFA's with many states, some of which are
performing the same function and can be combined. This is a necessary step in
generating a lexical analyzer since there may be hundreds of states in the
table for the tokens in a programming language.
A purist
would not consider the above automation a true DFA since a true DFA will have a
transition somewhere upon reading any character in the alphabet. Thus, state 0'
should have an arrow (leading to an "error" state) upon reading a
letter or a digit.
2.2.3 Lexical Analyzer
Generator Step 3:
Conversion to a Minimal DFA
Minimizing
a DFA consists of merging states which perform the same action. They can be
found by repeated partitoning. We will show this for an NFA in table form.
Final states 2 and 4 are shown in boldface:

The first
step is to partition the table into final and non-final states:

The
partioning continues by partitioning out states that lead to the same partition
for the same input. Here, states 1, 3, and 5 lead to the last partitioned state
upon reading a "$", while state 0 does not, so we put state 0 into a
new partition:

All states
in the second partition go to the same partition upon reading a letter or
digit, and they all go to the third partition upon reading a "$".
Thus, we are done, and relabeling the state table yields:

This
concludes the minimization step (see Exercise 8 )and
the procedure for conversion of a regular expression to a minimal finite
automation, that is, we have described a lexical analyzer generator.
2.4 Error Handling
The only
errors appropriately handled by a lexical analyzer are those which misuse a
sequence of characters. Errors such as using a reserved word as an identifier
are syntax errors to be found by the parser.
One way to
handle errors is to define error tokens. For example, if the language does not
contain a ".", a regular expression can be defined using one and the
associated action would be to report an error.
Anticipating
such user errors has met with limited success.
2.5 Generating a Lexical
Analyzer vs.
Writing a Lexical Analyzer
The reader
may think it is much harder to write a lexical analyzer generator than it is
just to write a lexical analyzer and then make changes to it to produce a
different lexical analyzer. After all, most programming languages have similar
tokens. This thought has been voiced by many compiler experts. In fact, many
compiler tools allow the user to write lexical analyzer and call it from the
generated parser or to make changes to a lexical analyzer provided by the tool.
Nevertheless,
the process is informative, and there may be applications for which the user
may wish to be able to generate various lexical analyzers.
The next
section shows an example of a lexical analyzer generator, LEX (Lesk and
Schmidt, 1975), a tool which comes with UNIX.
2.6 LEX, A Lexical Analyzer
Generator
This
section describes LEX, a lexical analyzer generator, written by Lesk and
Schmidt at Bell Labs in 1975 for the UNIX operating system. It now exists for
many operating systems, and versions can be obtained for almost any system
including microcomputers. The discussion here is for illustration and should
not be considered sufficient to use LEX.
LEX
produces a scanner which is a C program (there are versions which produce other
languages) that can be compiled and linked with other compiler modules. Other
LEX-like tools exist which generate lexical analyzers in Pascal, Ada, C++, etc.
LEX
accepts regular expressions and allows actions, code to executed, to be
associated with each regular expression. At scan time, when an input string
matches one of the defined regular expressions, the action code is executed.
The Lex Metalanguage
The LEX
metalanguage input consists of three parts: (1) definitions which give names to
sequences of characters, (2) translation rules which define tokens and allow
association of a number representing the class, and (3) user-written procedures
in C which are associated with a regular expression. Each of these three
sections is separated by a double percent sign, "%%". The input has
the following form:
Definitions (Gives
names to sequences of characters)
%%
Rules (Defines tokens. Class may be returned as a #)
%%
User-Written Procedures (In C)
The
Definition section consists of a sequence of Names, each followed by
an Expression to be given that name.
The Rules
consist of a sequence of regular expressions, each followed by an (optional)
action which returns a number for that regular expression and performs other
actions if desired, such as installing the characters in the token into a name
table.
The
User-Written Procedures are the code for the C functions invokes as actions in
the rules. Thus, the form for each section is:
Name1
Expression1
Name1 Expression1
...
%%
RegExp1 {Action1}
RegExp2 {Action2}
...
%%
C function1
C function2
...
A section
may be empty, but the "%%" is still needed.
Like UNIX
itself, the metalanguage is case-sensitive, that is, "A" and
"a" are read as different characters.
Example 4
shows a LEX description for our language consisting of assignment statements.
There are other ways of expressing the tokens described here.
2.6.2 Functionality of LEX
The C code
scanner generated by LEX can be altered before it is compiled. The generated
scanner is actually written to be "parser-driven"; when it is
integrated into a compiler front end, it is invoked by the parser.
Figure 3
shows how the tool operates. These steps may vary from system to system:

The LEX
metalanguage description is input in a file called lex.1. LEX produces
a file called lex.yy.c. The generated lexical analyzer is in UNIX's
executable file called a.out.
Within the
generated lex.yy.c is a C function called yylex() which
performs GetChar and other actions discussed in Section 2.2
The
resulting scanner matches the longest input sequence. If two regular
expressions match a particular input, then the first one defined is used. There
are many more details of LEX's functionality to be described, and the reader is
invited to look at a user's manual for
any available LEX to which you may have access.
2.7 Summary
This has
been an introduction to lexical analyzer generators and the process of
converting from a regular expression to a minimal DFA, which is the lexical
analyzer. This conversion is so complicated that many computer scientists
advocate writing a lexical analyzer and then making changes to it for new
applications. This works well for applications where the tokens are quite
similar.
The
process of generating a lexical analyzer has been likened to the compiler
process itself:

There are several lexical analyzer generators
on the market, making it unlikely that anyone except a compiler tool designer
or student in a sadistic instructor's class would ever have to write one.