Example 4

     P = Program

     U = Statements

     S = Statement

     A = Assignment Statement

     E = Expression

     T = Term

     F = Factor

and with left-recursion and common prefixes removed:

     P U

     U S U'

     U' | U

     S A;

     A Id := E

     E T E'

     E' + T E' |

     T F T'

     T' * F T' |

     F (E) | Id

     The (magically created) table contains a row for each nonterminal and a column for each terminal. Here, we show only the part of the token needed to make the decision. All Id tokens are the same, but operator tokens have to be shown individually, since the parse is different for different operators.

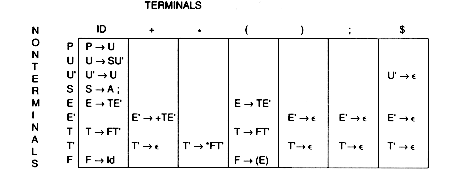
     The input string is:

     a := b * c + d ;

     Following the steps in the algorithm:

     (1) P is first pushed onto the stack. Since there is now a nonterminal on the top of the stack, the choice of nonterminal in the Case statement is taken. The current input symbol is a, which is an Id. We therefore consult the table at Table[P, Id] which contains the production P U. In (2), we replace the P at the top of the stack with U:

Stack                                                                  Input                                                 Production

(1) $ P                             a := b * c + d ; $                 P U

(2) $ U                             a := b * c + d ; $

     With the top of stack, U, we consult the table at Table [U, a ]. The production there is U S U'. We pop the top of the stack and replace it with S U' (with S on the "top"):

(2) $ U                              a := b * c + d ; $                 U S U'

(3) $ U' S                          a := b * c + d ; $

     Continuing,

$ U' S                                 a := b * c + d ; $              S A ;

$ U' ; A                              a := b * c + d ; $                    A Id := E

$ U' ; E := Id                         a := b * c + d ; $

     Now, the terminal option in the CASE statement is chosen since the top of the stack contains a terminal. This is matched with the first terminal in the input, and the stack is popped as the input is advanced:

$ U' ; E :=                        :=b * c + d ; $

     The top of the stack is a terminal which matches the input. The stack and input become:

$ U' ; E                      b * c + d ; $

Continuing,

$ U' ; E          		 a * b + c ; $             E T E'


$ U' ; E' T       		 a * b + c ; $             T F T'


$ U' ; E' T' F    		 a * b + c ; $             F Id


$ U' ; E' T' Id   		 a * b + c ; $


$ U' ; E' T'     		 * b + c ; $               T' * F T'


$ U' ; E' T' F *      		* b + c ; $


$ U' ; E' T' F           	b + c ; $                  F Id


$ U' ; E' T' Id          	b + c ; $ 


$ U' ; E' T'                	+ c ; $                   T'  


$ U' ; E'                   	+ c ; $                   E' + T E'


$ U' ; E' T +                	+ c ; 


$ U' ; E' T                  	c ; $                     T F T' 


$ U' ; E' T' F                  c ; $                     F Id 


$ U' ; E' T' Id                 Id ; $ 


$ U' ; E' T'                    ; $                       T' 


$ U' ; E'                       ; $                       E' 


$ U' ;                          ; $ 


$ U'                            $                         U' 


$                               $


Accept!