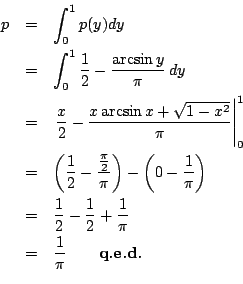Proof:
The proof is not particularly rigorous but works. We will consider only one crack between two planks since it won't change the result. Consider Figure 1, in which the thick line is the needle and we consider only the case in which the needle falls across the upper crack.
The needle falls at a random location, i.e., ![]() has uniformly
distributed coordinates
has uniformly
distributed coordinates ![]() and
and ![]() . Since the planks are infinitely
long, we do not need to consider the
. Since the planks are infinitely
long, we do not need to consider the ![]() -coordinate. As for
-coordinate. As for ![]() , we
will consider only the case in which the distance between
, we
will consider only the case in which the distance between ![]() and
the upper crack in the figure is not bigger than
and
the upper crack in the figure is not bigger than ![]() since otherwise
the needle can not fall across the crack. We do not need to consider
the other case, in which the needle falls in the lower half of a
plank, since it is a mirror-image of our case, and therefore the
probability will be the same as for our case. Also, those events are
independent from each other, since the needle can never fall across
two cracks at the same time.
since otherwise
the needle can not fall across the crack. We do not need to consider
the other case, in which the needle falls in the lower half of a
plank, since it is a mirror-image of our case, and therefore the
probability will be the same as for our case. Also, those events are
independent from each other, since the needle can never fall across
two cracks at the same time.
Note that the needle falls at a random location and at a random
angle ![]() . We measure the
. We measure the ![]() -coordinate as distance from the
crack. Thus,
-coordinate as distance from the
crack. Thus, ![]() is uniformly distributed between
is uniformly distributed between ![]() and
and ![]() , while
, while
![]() is uniformly distributed between
is uniformly distributed between ![]() and
and ![]() . To simplify
the proof, we will set
. To simplify
the proof, we will set ![]() without loss of generality.
without loss of generality.
Now, the probability that the needle falls across the crack for a
certain ![]() is
is ![]() . It is clear from the picture
that
. It is clear from the picture
that ![]() and that
and that ![]() for all
for all
![]() . Therefore,
. Therefore, ![]()
Considering that ![]() is uniformly distributed between
is uniformly distributed between ![]() and
and ![]() , we
can now simply find the integral for
, we
can now simply find the integral for ![]() in the interval
in the interval ![]() to
get the probability
to
get the probability ![]() . Note that
. Note that ![]() .
.