Extended Euclidean Algorithm

If you like a challenge, try to find an equivalent algorithm yourself instead of simply using this one. That is essentially Problem 7.31 in the textbook. The recursive form is easier to find and can be ``flattened out'' into an iterative form quite easily.

Input: positive integers $a$ and $b$.

Output: integers $x$ and $y$ such that $\gcd (a,b)=xa+yb$.

This algorithm is often used to compute the inverse of number $b$ modulo number $a$ (i.e., computes $y$ such that $by\bmod a=1$). This works if and only if $\gcd(a,b)=1$, otherwise $b$ does not have an inverse modulo $a$. For more hints, see book Problem 7.31 or Prof. Paar's script.

ext_euclid(int a, int b)
   x:=1; v:=1; y:=0; u:=0;
   do
     q := a div b; // integer division
     r := a mod b;
     a := b; b := r; // this is the standard Euclid
     x_tmp := x; y_tmp :=y;
     x := u; y := v;
     u := x_tmp-q*u; v := y_tmp - q*v;
  while (b>0);
return x,y

Example: $\textit{ext\_euclid}(60,7)$

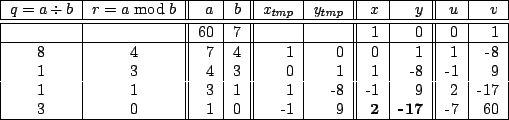
which means:

$\gcd(60,7)=2\cdot 60 - 17\cdot 7 = 1$

Hint: For RSA, $y$ represents the component $s$ in $k_{pr}=(p,q,s)$, therefore it must be positive to be used as an exponent in decryption. If the algorithm produces a negative number for $y$, as in this example, just add $a$, since everything is modulo $a$. In this example, the $y$ returned is $-17$ which modulo 60 is equivalent to $43$.

So in arithmetics modulo 60 (for RSA, that could be $p=7,q=11$, so $\phi=(p-1)(q-1)=60$), if you choose $7$ as your public key, the private key is $43$. $43$ is the only number less than $\phi$ that, multiplied with $7$ modulo $\phi$, is 1. Convince yourself that this is true. Therefore, by our theorems, $(a^7\bmod 77)^{43}\bmod 77=a$ for all $0\leq a<77$, so $k_{pub}=(z,n)=(77,7)$ and $k_{pr}=(p,q,s)=(7,11,43)$.