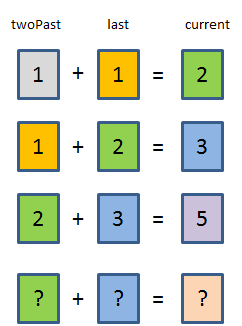CS 110X Jan 23 2014

Lecture Path: 04
Back Next

Expected reading: pages 40-50.
Expected interaction: For loops
Clicker: Assessment

Draft List of Programming Partners Now Available

Roark got up, reached out, tore a thick branch off a tree, held it in both hands, one fist closed at each end; then, his wrists and knuckles tensed against the resistance, he bent the branch slowly into an arc. "Now I can make what I want of it: a bow, a spear, a cane, a railing. That’s the meaning of life."
"Your strength?"
"Your work." He tossed the branch aside. "The material the earth offers you and what you make of it..."
The Fountainhead, Ayn Rand

1 Rinse. Lather. Repeat

You have a collection of comma-separated values and you want to know how many elements are in the collection.

In fact, you find yourself faced with this task dozens of times during the day. Sometimes the collection has five values; sometimes it has 50. You want to find a way to eliminate this tedious task.

Q1: Write a program that prompts the user to enter in values separated by commas, and the output is the number of values.

1.1 Manual

This is not a challenging task after all; just tedious.

Given a collection, you count the first value as ’1’, then the second value (after the comma) as ’2’; you continue until you run out of values.

1.2 Programming

How are you going to do this using Python? At this point, you know how to read a single value, just one at a time. Also, we only have the ability to execute a sequence of Python statements, one after the other until a function (or module) ends. In this lecture you will learn some key concepts that will help answer the problem.

1.3 Lists

In all of our examples, we have used a variable to store a single value. This approach will fail, for example, when you want to store a group of related values. For example, assume I have just graded the final exams for a class of 30 students, and I want to compute the class average. To do this right now, I would have to create 30 separate variables – f1, f2, ..., f30 – each storing the grade of a specific student. Then the average would be defined as avg = (f1 + f2 + ... + f30) / 30.0.

What an inefficient way to operate! Instead I would want to have a single variable, called finalExams, that would somehow store all exam grades for all students.

We can do this in Python using a list (which is similar to an array as found in numerous programming languages).

Let’s define a list, temps, that contains the high temperatures forecast for the next five days:

temps = [ 34, 46, 43, 39, 39]

A Python list is identified by a starting left-bracket ([) and a closing right-bracket (]). Between these two brackets may be any number of Python values separated by commas (,).

The following are all valid lists:

L1 = [ 1, 2, 3 ] # a list of int values L2 = [ 1.3, 3.4, 99.4 ] # a list of float values L3 = [] # an EMPTY list containing no values L4 = [’go’, ’patriots’ ] # a list of strings by a pats fan

You will learn many useful operations over lists, here is one:

To find out how many values are stored in a list, use Python’s len(...) function. Using the above lists:

>>> len(L1) 3 >>> len(L2) 3 >>> len(L3) 0

When given a list of values, often we would like to perform some computation over every element in the list. For example:

average all elements in the list
"Start with sum=0. Then for each element, x, in the list, add x to sum. When done, divide sum by the number of elements in the list."
find the sum of the elements in the list
"Start with count=0. Then for each element, x, in the list, add 1 to count."
find the product of all elements in the list
"Start with product=1. Then for each element, x, in the list, multiply product by x."

Each of these operations is easy to explain, and as you will find, easy to code once you understand the definite for loop.

1.4 Definite for Loop

If only we had some way to repeat a sequence of Python statements! Naturally, since you have been reading the text book, you should have seen the for statement.

The following, for example, will print out the elements of a list, from the first (left-most) one to the last (right-most) one.

>>> L4 = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29] >>> for x in L4: print (x)

The first thing to observe is that once you type the colon (:), the IDLE Python editor auto-indents statements. This tells you that the for statement is expecting a sequence of statements.

Second, you need to associate a variable (in this case x) that changes with each pass through the loop to contain each successive element in the original list.

Third, this sequence officially closes when you enter a blank line (by pressing RETURN/ENTER). At that point, the code executes, and it prints out the first ten prime numbers, one at a time, one per line.

Note that all indented statements in a for loop are executed in order, and the iterating variable (in this case, x) is set to each subsequent element in the sequence (in this case, L4) prior to the execution of these indented statements.

To "read" the above program in English, you would say to yourself:

Assign L4 to be the 10-member list composed of values 2, 3, 5, ... for each value in L4, print value

You can see how closely the Python syntax mirrors the actual English sentences above.

1.5 Quick Assessment

Just so we are clear regarding indented statements, what does the following code output? Try to work it out for yourself before typing this code into a Python Shell window.

Press To Reveal

>>> L4 = [2, 3, 5] >>> for x in L4: print (x) print (x+1)

Output

If you reveal the output on the right, you should see how the indented statements are both executed during each "pass" of the loop.

To complete this section, the following code simply counts the number of values in a list.

>>> L4 = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29] >>> count = 0 >>> for x in L4: count = count + 1 >>> print (count) 10

Another way to understand the for loop above is to think about the statements that execute:

L4 = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29] count = 0 x = 2 count = count + 1 x = 3 count = count + 1 x = 5 count = count + 1 x = 7 count = count + 1 ...

And these statements execute until x has iterated over all elements in L4.

1.6 Reading A List As Input

To complete our initial problem, we need to present the means for the user to enter in a list. If we could do this, we can use the for statement as shown earlier.

Let’s assume you can change the behavior of the person entering in the values. That is, instead of just a comma-separated sequence of values, you can ask the user to start with a "[" and then close with a "]".

As I’ve tried to explain very carefully, the input Python statement reads values from keyboard input. And since a list is defined to be bracketed by "[ ... ]" characters, you can take advantage of this to simplify your program.

>>> temps = input("Enter a list of values [a, b, c, ...] ") Enter a list of values [a, b, c, ...] [ 34, 46, 43, 39, 39] >>> print (temps) [ 34, 46, 43, 39, 39]

Recall how I mentioned that input allows the user to enter in a Python value? Well, a list is a kind of Python value.

1.7 Explanation

The final (rather short) program appears below:

# Lecture Example: # Author: George Heineman theList = input("Enter a list of values [a, b, c, ...] ") count = 0 for v in theList: count = count + 1 print (str(count) + " values were entered.")

Type this into a Python Shell window to see it working in action.

1.8 Looping An Arbitrary Number Of Times

The previous examples show how you can iterate over each element in a list. There are times when you just want to execute a sequence of statements a fixed number of times. For example, to print the numbers from 1 to 10, together with an accumulating sum, you could do the following:

print (str(1) + "," + str(1)) print (str(2) + "," + str(3)) print (str(3) + "," + str(6)) print (str(4) + "," + str(10)) print (str(5) + "," + str(15)) print (str(6) + "," + str(21)) print (str(7) + "," + str(28)) print (str(8) + "," + str(36)) print (str(9) + "," + str(45)) print (str(10) + "," + str(55))

Of course, you must imagine there is a better solution. If you review the above statements, you will see that what varies are the number and the partial sum. If only you could say something like the following

repeat the following statement for n in {1, 2, ..., 10}: keep running total of values for n print n , total

If this is done right, these indented statements would be executed a fixed number of times, and thus provides a convenient short-hand to the program above.

As it turns out, you can.

Recall that during "calculator mode" in the Python shell you can see the immediate values of computations? Well, type the following function call:

>>> range(1,11) [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

As you can see, the the range function call creates a list. You can tell that it is a list because it contains a comma-separated list of values bracketed by "[" at the left and "]" on the right.

To solve the earlier problem using a for loop, then, you would write the following Python code:

total = 0 for i in range(1,11): total = total + i print (str(i) + "," + str(total))

Not only is this code more concise, it can easily be modified to work with larger sequences. This loop, in essence, computes the following statements:

total = 0 i = 1 total = total + i print (str(i) + "," + str(total)) i = i + 1 total = total + i print (str(i) + "," + str(total)) i = i + 1 total = total + i print (str(i) + "," + str(total)) i = i + 1 total = total + i print (str(i) + "," + str(total)) ...

This computation continues until the value of i reaches 11, which then terminates the loop.

I hope you can see that using range allows you the same behavior as shown earlier when iterating over elements in a list.

So now the only issue is to explain why you need to use range(1,11) to produces ten numbers. Let’s try some examples:

>>> range(4,7) [4, 5, 6] >>> range(-3,4) [-3, -2, -1, 0, 1, 2, 3]

So it looks like range(a,b) gives you a list containing b-a numbers ranging from {a, a+1, ..., b-1}.

To put this in English, the Python statement range(a,b) produces a list of consecutive integer values from a up to but not including b. To use mathematical notation, range(a,b) reflects the interval [a, b) which is "closed" on the left, but "open" on the right.

As a quick aside, Python also allows range(b) function calls, which return the list of numbers from 0 up to but not including b, such as:

>>> range(10) [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Counting from zero is common in both mathematics and computer science. We have to get this concept squared away, because it will arise in other areas as well.

1.9 Fibonacci Numbers

To complete our lecture on the definite for loop, you can apply the looping style above to complete the first n Fibonacci numbers.

As you may know, the Fibonacci numbers are an additive series where the first two Fibonacci numbers are F1 = 1 and F2 = 1. You can compute any Fibonacci number Fn by adding together the two previous Fn-1 and Fn-2 Fibonacci numbers.

Based on this definition, you can actually write a small program to print out Fibonacci numbers. To get started, look at the following image in which time is represented vertically:

Figure 1: Fibonacci Explanation

If you review the above, it is possible to compute the current Fibonacci number by adding together the last one with the twoPast one. To make this work, all you have to do is update what you mean by these two values.

Can you see that you are essentially completing a repetitive process? As long as you do your own bookkeeping, this is something you can do in a small program, such as following:

def printFibonacci(): twoPast = 1 last = 1 # don’t forget to print out first two print (twoPast) print (last) # loop computes next Fibonacci numbers # here variable ’i’ is never used in the computation # it is only used to count how many times to # perform this loop for i in range(10): current = twoPast + last print (current) # be sure you understand why these two # statements have to be in this exact order twoPast = last last = current

1.10 Debugging Challenge

We’ve covered a number of topics in this lecture. Let’s get to the debug challenge! Please review this challenge in preparation for tomorrow’s lab exercise.

An old story relates how when Gauss was a child, he came up with an immediate way to compute the sum of the numbers from 1 to n. The following tries to validate this approach for n = 100 using Python. Unfortunately, there are six syntax and logic defects. Can you find them all?

Press To Reveal

# Author: Carl Friedrich Gauss n = 1 for i in range(1,n): total = total + 1 print ("The following numbers should be the same’) print (total) print (n * n+1 / 2)

Defects

1.11 Skills

You learned how to construct a definite loop. The first type is with a pre-specified range, such as range(15), which covers numbers 0..14. The second type is when iterating over elements in a sequence. So far the kind of collections you have seen include:

string literal – a sequence of characters
a list – a sequence of values, identified as [v1, v2, ..., vn], that can be grow or shrink, or allow individual values to be changed.

New skills introduced include:

CS-9. Write definite for loop
DT-10: Know how to iterate over elements of a list

1.12 Self Assessment

This questions extends the assessment you wrote using the Ideal Gas Law.

Instead of computing for n, assume that you know the following two parameters: Temperature = 20 degrees Celsius and n = 0.029 moles.

Compute a table showing the changes in Pressure, P, given corresponding changes in Volume.

That is, for volumes in the range 0.10 litre to 2 litre in steps of 0.10, how does the pressure, P, change?

Hint: the range function generates integer lists. Do you see how range(1,21) would actually be useful here?