Complete

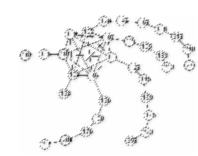
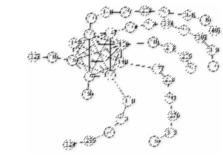
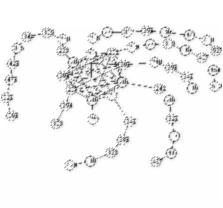
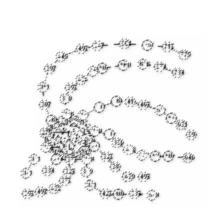
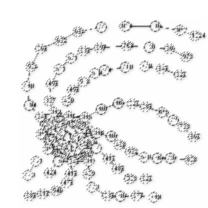
These graphs were generated using an algorithm that transforms a complete graph Kn into an SI graph.

Graph Description Thumbnail Path Edges
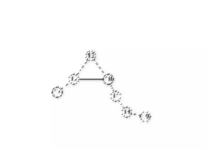
7_Vertices_7_Edges_K3.gif T7_V.jpg (1964 bytes) <0,1,3>
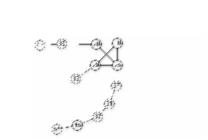
12_Vertices_14_Edges_K4.gif T12_V.jpg (2495 bytes) <0,2,1,5>
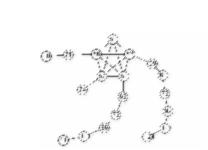
19_Vertices_24_Edges_K5.gif T19_V.jpg (3255 bytes) <0,2,1,5,6>
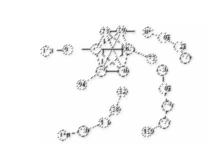
24_Vertices_33_Edges_K6.gif T24_V.jpg (3887 bytes) <0,2,1,5,6,4>
32_Vertices_46_Edges_K7.gif T32_V.jpg (4878 bytes) <0,2,1,5,6,4,7>
41_Vertices_61_Edges_K8.gif T41_V.jpg (5877 bytes) <0,2,1,5,6,4,7,8>
51_Vertices_78_Edges_K9.gif T51_V.jpg (7056 bytes) <0,2,1,5,6,4,7,8,9>
62_Vertices_97_Edges_K10.gif T62_V.jpg (7482 bytes) <0,2,1,5,6,4,7,8,9,10>
74_Vertices_118_Edges_K11.gif T7_V.jpg (1964 bytes) <0,2,1,5,6,4,7,8,9,10,11>
Does this trend continue?  

See hypothesis below

Hypothesis

For k >= 7, construct a graph G around a complete graph Kk such that (in counter clockwise fashion), linear arms are constructed outwards from each node in Kk to be of length <0,2,1,5,6,4> for the first six nodes while the remaining (k-6) nodes have paths of length 7+i for i = 1 to k-6.

Miscellaneous

Graph Description Thumbnail
26_Vertices_34_Edges_K4_K5.gif 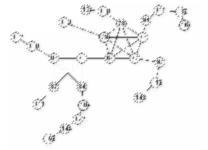TK4_K5.jpg (4155 bytes)
CrazyAdditions_K4.gif

Recursive

Graph Description Thumbnail
17_Vertices_19_Edges_K3_recursive.gif 17_V_19_E_K3.jpg (3807 bytes)
21_Vertices_23_Edges_K3_recursive.gif 21_V_23_E_K3.jpg (4203 bytes)
24_Vertices_31_Edges_K4_perfect_recursive.gif 24_V_31_E_K4_perfect_recursive.jpg (5404 bytes)
24_Vertices_31_Edges_K4_recursive.gif 24_V_31_E_K4_recursive.jpg (4864 bytes)
24_Vertices_32_Edges_K4_recursive.gif 24_V_32_E_K4_recursive.jpg (5198 bytes)
36_Vertices_49_Edges_K5_recursive.gif 36_V_49_E_K5_recursive.jpg (6351 bytes)
38_Vertices_52_Edges_K5_perfect_recursive.gif 38_V_52_E_K5_perfect_recursive.jpg (6841 bytes)

 

Cycle

Nothing

Chains

Chains

Mesh

Mesh

High Degree

Is there a maximum degree for a status injective graph? For example, there can't be two nodes with degree n-1 since they would both, then, have the same status value (n-1). While there is no clear answer to this question, here are some graphs that show empirical results.

Try 3

Name MaxDegree NumVertices Added subgraphs Ratio sqrt(2n-1) sqrt(n)
Phase0 3 7        
Phase1 4 12 <3,0> 3 4.795832 3.464102
Phase2 6 16 <2,0> 2.666667 5.567764 4
Phase3 8 30 <12,0> 3.75 7.681146 5.477226
Phase4 10 47 <15,0> 4.7 9.643651 6.855655
Phase5 12 59 <10,0> 4.916667 10.81665 7.681146
Phase6 14 78 <17,0> 5.571429 12.4499 8.831761
Phase7 16 91 <11,0> 5.6875 13.45362 9.539392
Phase8 18 101 <8,0> 5.611111 14.17745 10.04988

The upper bound must be higher than sqrt(2n-1). Without any theory to go on -- simply the results from the graphs in phase 2 and beyond that increase the max degree by 2 -- the max degree may be best expressed as: dmax = (7*n+189)/51. These odd numbers come from the trendline when calculated within excel that gives R value of .9956 for the equation 51/7*dmax - 27 = n.

See stats.xls for details.

Try 2

Another approach seeks to add complete graphs around a central target node, thus creating a high degree node within an SIJ. The following table shows the results.

max deg n |E| Long Path Ratio
Phase1 3 7 7 3 2.333333
Phase2 6 20 23 9 3.333333
Phase3 10 37 46 10 3.7
Phase4 15 60 79 12 4
Phase5 21 96 130 20 4.571429

See stats.xls for details. Results (for converging trend lines) are similar to Try 1 below.

Try 1

Again, similar to Try 2.

max deg. n |E| Longest Spine sum stat ratio: n/max ratio: n/|E|
Phase1 1 2 1   -- not SI --    
Phase2 3 5 5 1 -- not SI --    
Phase3 6 11 14 2 250 1.83333333 0.785714
Phase4 10 21 30 3 1220 2.1 0.7
Phase5 15 38 57 6 5468 2.53333333 0.666667
Phase6 21 62 96 8 18152 2.95238095 0.645833
Phase7 28 103 158 19 78992 3.67857143 0.651899

The upper bound has a quadratic formula to show its max value. In short form, one can see that dmax is no greater than 3.36 * sqrt(n).

See stats.xls for details.