An Amida Board B = { L, E} is defined by a sequence of N = |L| lines (ordered left to right as L1 .. LN) and a set of M = |E| cross-edges connecting lines Li and Li+1 at a vertical position y. Thus a line Ej can be uniquely identified by the triple (i, i+1, y). The vertical position is a positive integer >0 and is referenced by the notation L.y, the two lines are L.left and L.right.
Definition: An Amida board has unconnected lines (Li Li+1) if there is no edge Ej in the set E such that (Ej.left = i) and (Ej.right = i+1).
Definition: An Amida board contains two negating cross-edges Ej and Ek (without loss of generality, assume Ej.y < Ek.y) if (A) Ej.left = Ek.left and Ej.right = Ek.right; (B) no edge Em exists such that (Em.right = Ej.left) and (Ej.y < Em.y < Ej.y); and (C) no edge Em exists such that (Em.left = Ej.right) and (Ej.y < Em.y < Ej.y);
Definition: A Regular Amida Board has no (1) unconnected lines; (2) negating cross-edges; or (3) cross-edges with the same vertical position. The last condition (3) can easily be assured by simply expanding the edges of the board without affecting its outcome. Assuming this third property makes some of the definitions and algorithms clearer.
Given any Amida board, it can be 'stretched out' so each cross-edge Ei has a unique y value without altering the outcome of the board. One can form a sequence of edges from the top of the board (lowest y value) to the bottom of the board (highest y value); each of these edges can be selected independently from the set of (N-1) potential cross edges that can be added at that y location. Therefore, there are a total of (N-1)W unique Amida boards. However, these Amida boards are not guaranteed to be regular.
Given M cross-edges to be placed, we need to at least place N-1 to ensure the board has no unconnected-lines. These N-1 cross-edges can be placed (N-1)! possible ways, since the y positions of these N-1 edges must all be different. There are (M-(N-1)) edges, or M+1-N, edges left to be added, and these can be placed in N distinct "regions" (formed by the spaces between the N-1 edges placed to ensure a connected Amida board.
....
There are (M-(N-1)) edges, or M+1-N, edges left to be added. The ith of these edges (0 < i < M+1-N) to be added must have a different y position from the existing (N-2+i) edges in the board, thus there are N-1+i possible values it could have. In addition, these edges can be placed between different edges, but we must ensure that we do not add a negating edge. There are a total of (N-1)*(N-1+i) potential places to place the cross edge. Of these locations, a negating edge would occur 2*(N-2+i) times (for each of the existing edges, a negating edge would exist just above and just below it). Thus we can add in the following potential locations:
(N-1)*(N-1+i) - 2*(N-2+i) =
(N-1)2 + i*(N-1) -
(2*N-4+2*i) =
(N-1)2 + i*N - i - 2*N + 4
- 2*i =
(N-1)2 + (i-2)*N + (4 - 3*i)
=
N2 + (i-4)*N + 5-3*i
So we start with N-1 edges (for a total of (N-1)! potential graphs). Then we grow by multiplying possible additions:
#Amida = (N-1)! * PRODUCT<i=1..M+1-N> (N2 + (i-4)*N + 5-3*i)
Working from Maple, this computes to be:
 |
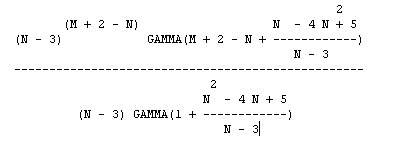
Which approximates. Top internal polynomial limits to (M+2-N-4) and bottom to (1+N), leading to
|
(N-3)(M+2-N) * (M-N-2)! (N-3) * (N+1)! equals: now (M-N-2)! = ((M-1) - (N+1))!, thus the ratio (M-N-2)!/(N+1)! is <= (M-1)! we now have a rough upper bound on the number of regular Amida graphs with N lines and M cross-edges. (M-1)! * (N-3)(M+1-N) |
We must be careful not to over-count. For example, with N edges to add, there are two distinct ways that these could be added. Thus, we must amortize based upon the total number of cross-edges found in a single column.