by Curt Ferguson

Introduction         Modeling human characteristics is one of the most difficult and challenging issues in today’s computer graphics. One of the most difficult characteristic is the modeling of realistic hair. In the late 1980s new techniques appeared in an effort to create realistic hair models. These models were only for creating furry objects, such as teddy bears, and spiders. By using variations of these techniques it is possible to create realistic hair models. Why develop a method for rendering Human Hair?         Photorealistic human images depend largely on realistic hair. Problems:         Given the extremely large total number of hairs on a human head, obtaining results within a reasonable amount of time proves difficult.          The 3d shape of hair is complicated. With conventional methods an enormous number of patches are required to render even a simple hairstyle.

[4]

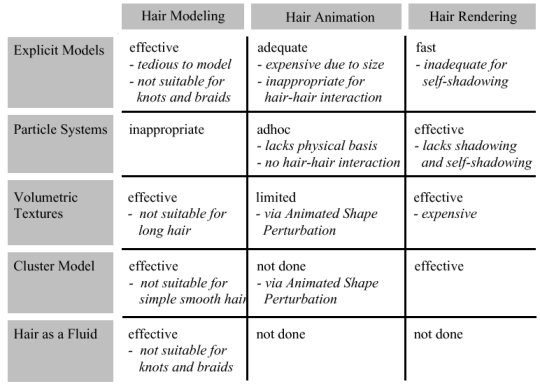
Current techniques There are currently 5 techniques used for hair rendering [4]. Explicit Models Particle systems Volumetric Textures Cluster Models Fluid Models

Explicit Model

• A differential equation method is used for modeling the aesthetic features of human hair.

• A cantilever beam simulation is employed for hairstyle modeling, which allows hairdressing variations with volumetric and realistic appearance.

• the dynamical behavior of hair as an animation is described through one-dimensional projective differential equations of angular momenta

• Individual hairs are represented as linked rigid sticks.

• A "rough" approximate solution is provided for collision detection between hair and a human head by solving the projective equations under a pseudo-force field.

• The hair’s pliability can be controlled by using a set of stiffness parameters in the method.

• Blinn’s specular model is used as a fast rendering technique.

Prior knowledge

        Prior knowledge on hairstyling is the hairstyle modeling techniques and steps involved in actual styling.  When we are creating a method to model hairstyling, both artificial and intrinsic properties must be considered.  In the hair styling of real hair a stylist uses many artificial techniques, such as shearing, perming and combing, to get the desired hairstyle.  The intrinsic properties of the desired hairstyle are selected. These are either added or already included, as the natural and physical properties of the hair (color, width, pliability and volumetric appearance).

        Physically based modeling approaches are not considered.  The reasoning is that physically based modeling approaches contain to many variables.  In particular it is impossible to numerically treat self-interaction or collision detection of a large amount of hair, typically tens of thousands.  For this reason, the hair is approximated as a series of cantilever beams.

Modeling Steps

Differential equation governing cantilever beam deformation:

Part 1: Define an ellipsoidal hull of the head model, which can be considered as a rough approximation to the head. Then also specify the region of hair pores on the ellipsoid.

Part 2: Calculate hair bending, based on a simplified simulation of a cantilever beam. This process also includes collision detection between each hair and the ellipsoid.

Part 3: Cut hair and modify with slight adjustment, in order to get the desired shape in the final stage.

Ellipsoidal Approximation

Advantages of Ellipsoidal Approximation:

• A polar coordinate system is available for an ellipsoid.

• Polar coordinates are an easy way to specify the hair locations for an ellipsoid.

• An ellipsoid also has the benefit of allowing collision detection at a low computational cost.

Compared to polygonal models:

• A regular polygonal representation does not have an easy method of specifying locations.

• Regular polygonal models have an inherently large polygon count.

• Regular polygonal models require collision detection for each polygon.

Hair Bending         Calculations for hair bending are performed as a simplified simulation of a cantilever beam.  Collision detection between each hair and the ellipsoid is also calculated         A cantilever beam is a straight beam with a fixed support on one-side.  To understand how to calculate the bending of an individual hair we must first look at it in two dimensions. We are going to use a cantilever beam representation for the hair.

[2]

Calculate Hair Bending

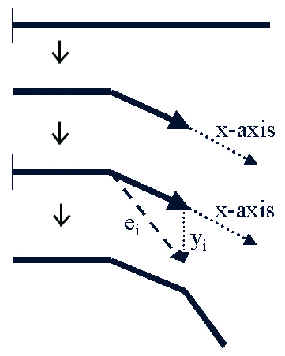
        A uniformly distributed external force g (gravity) is applied to the beam.  This produces a bending moment and shearing force.  Due to the small size of the beam, the shearing force can be ignored.  The x-axis of the lever is along the initial beam direction.  The y-axis is vertical to the direction of the applied force.  The y-axis represents the deflection direction of the beam. (Also considered the amount of sag for the beam)

Cantilever Beam

Equation of Deformation Process 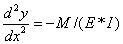          [Anjyo et al]

E is Young's modulus (Stress/strain)

I denotes the second momentum of area.

M is the bending moment per unit length (torque).

E*I is the flexural rigidity of the beam. This value depends on the material of which the beam is composed.

        As with the shearing force, this equation does not consider large deformations.  It is still valid for the deformation of hair though, as the hair is broken up into segments, each of which have little deformation.  The beam is separated into a finite number of linear segments with uniform lengths.  The distributed load g is approximated by the sum of segmentally averaged concentrated loads.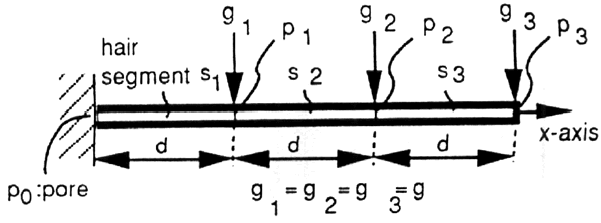[Anjyo et al]

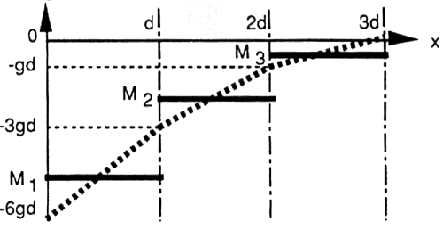
        The cantilever beam formula is further simplified by holding the bending moment constant.  Below, the dotted line is a physically accurate bending moment at x, while the solid lines are approximated positions.

[Anjyo et al]

Cantilever Beam Approximation Formula

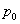        to 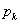are the node vectors of the hair segments.  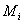is the constant bending momentum on segment .

       

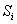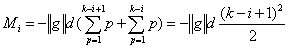
        The displacement 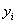of the node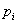is

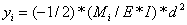
        Next, the two-dimensional method is applied in three dimensions.

Three Dimensions

Two dimensions	Three dimensions

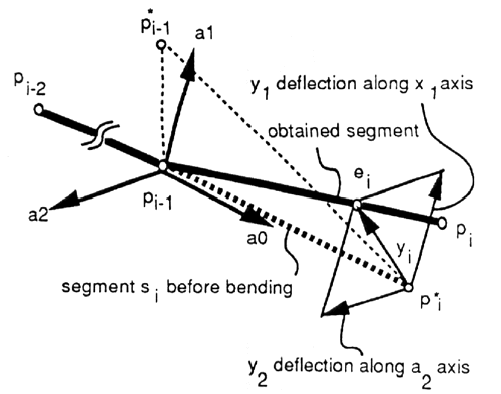        To do this, we must create a new coordinate system. The a0 axis corresponds to the x-axis that is described in the two dimensional case.

1. a0 axis is defined as the the segment vector pi-2 -> pi-1.

2. Point p*i is placed a certain distance along the a0 axis.

3. Reference point p*i-1 is set at a known distance from pi-1.

4. The a1-axis is vertical to the a0-axis on the plane spanned by these three points.

5. The a2-axis is orthogonal to both axis.

6. Apply the two dimensional method to obtain the deflections y1 along the a1-axis and y 2 along the a 2-axis. These deflections are obtained by using the respective component of the force.

7. The desired deflection of the vector yi is obtained as y1a1 + y2a2.

        Collision detection is also considered, but only between the hair and the head model, not between the individual hairs.  Anywhere from 100,000 to 400,000 individual hair segments and roughly 10,000 polygons are typically considered sufficient to model hair.  To calculate the collisions between a large amount of hair segments and polygons would require a high computational cost. This is where the ellipsoidal approximation comes in.  Any new points are checked to see if they lie inside the ellipsoid. If so, the point is simply moved to the outside of the ellipsoid.

        Hair is cut by restricting the beam length of polar coordinate regions to the desired hair lengths.  Hair is combed by adding additional external forces.

[Anjyo et al]

Dynamic Behavior A physics based model of hair properties is not optimal.  This is primarily due to the number of unknown functions in the derived differential equations need to recreate all the physical properties.  Another problem with a physically based model is the problem of dealing with the self-interaction between individual hairs, such as collision detection.  The number of calculations that are needed for these types of interactions between thousands of individual hairs are such that it would be infeasible to use a physically based model system         To simplify the process the inter-hair collisions are disregarded . By doing so we able to greatly lower the number of computations needed in order to recreate the behavior of hair.  We are also able to derive simple differential equations that avoid dealing with physically rigorous formulation, and only consider visual representations of the hair.          The dynamic behaviors of inertial momentum, hair stiffness, and dynamic collision are considered.

[Anjyo et al]

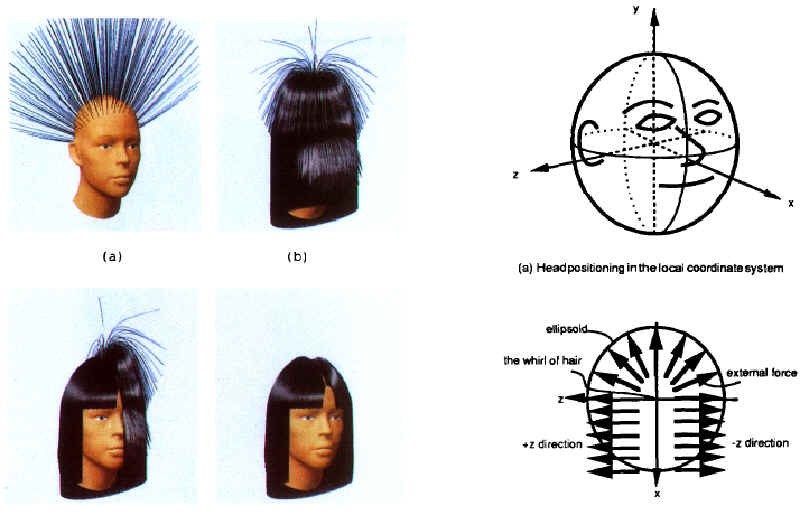
        Inertial momentum is an external force which can be applied over time and in varying amounts across the ellipsoid, giving the illusion of friction.  In the 4 pictures below, four images over time were taken of hair with inertial momentum. 

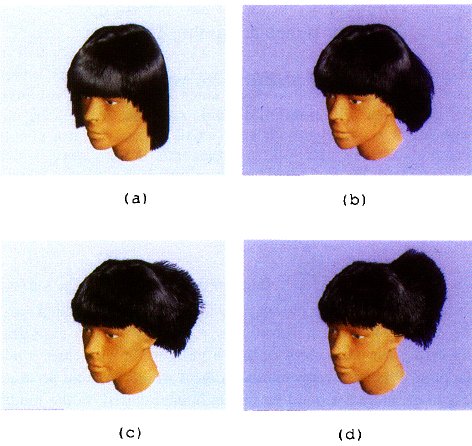
        The equations for finding the physical properties that simulate stiffness in hair are displayed below.  This is a simple process of controlling how much of a deformation angle the hair is allowed to bend.  The head on the right has a tuft of hair with higher stiffness the than rest, resulting in it extending further.

        A pseudo-force field is used to resolve dynamic collision avoidance.  This is done to keep the hair from colliding with the head during an animation.  Considered another external force

[2]

        The pseudo-force field is used to limit the effect that an external force has on the hair.  The closer the hair is to the head model the greater the pseudo-force is.  This method eliminates collisions between the hair and the head model.

The two techniques I saw used to render hair are ray tracing with Blinn's specular model and the Trigonal Prism-Based Method.  Blinn's specular model is designed to handle ray collisions with round objects.  As each hair segment is a cylinder with a very small radius, it works well.  The disadvantage of this method is that shadowing effect is disregarded.  The Trigonal Prism-Based Method represents each hair segment as a prism shaped cylinder, so can be modeled as 3 patched rectangles.  This method has the advantage of using  standard z-buffering techniques for rendering speed, but is not as detailed as ray tracing with Blinn's specular model.

        The paper by Anjya et al included much work on modeling the aesthetic features of human hair, focusing on hairstyling and dynamics.  However, it does not emphasize the rigorous physics necessary for modeling, instead using differential equations as the visual analogies.  Watanabe and Suenaga grouped multiple hairs into wisps, and represented the wisps as triangular patches.  This technique is does not achieve the same realism as Anjya et al, but grouping of hairs that will bend in the same direction greatly reduces the number of beams that must be solved for.  For anyone wishing to realistically render human hair, the methods of these two papers should provide all the information needed.

[1]Ken-Ichi Anjyo, Yoshiaki Usami, and Tsuneya Kurihara, "A Simple Method for Extracting the Natural Beauty of Hair", Proc. ACM SIGGRAPH 1992 ACM Paper Page

[2]K Babic, "Modeling Human Hair" CS 563 1999 Presentation Presentation Online

[3]R. Lu, J. Koederink and A. Kappers, "Specularities on Surfaces with Tangential Hairs and Grooves", IEEE International Conference on Computer Vision, pp. 2-7, 1999 IEEE pdf file

[4]N. M. Thalmann, S. Hadap, P. Kalra, State of the Art in Hair Simulation, International Workshop on Human Modeling and Animation, June 2000, Korea Computer Graphics Society, pp. 3-9 pdf file

[5]Yasuhiko Watanabe, and Yasuhito Suenaga, "A Trigonal Prism-based Method for Hair Image Generation", IEEE Computer Graphics and Applications, January 1992: 47-53 IEEE CG&A Paper Page