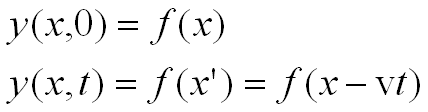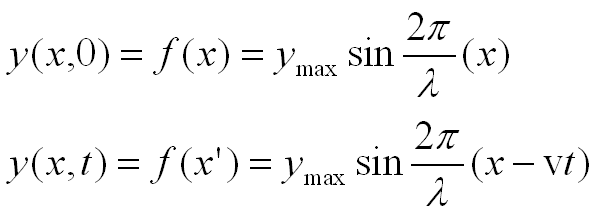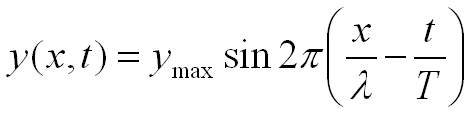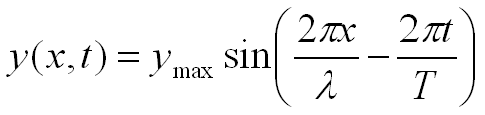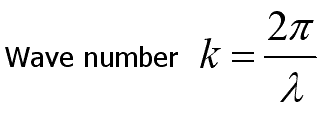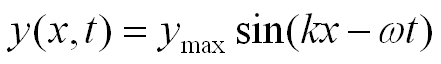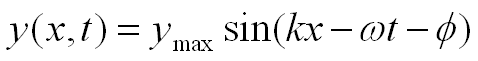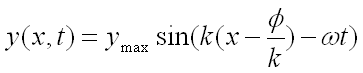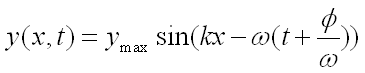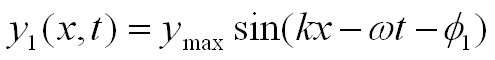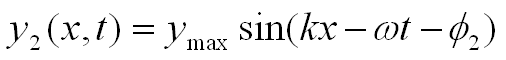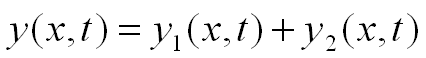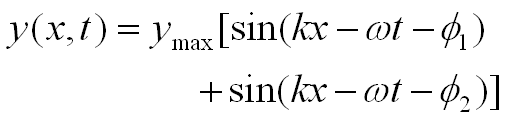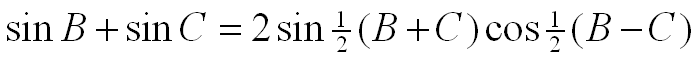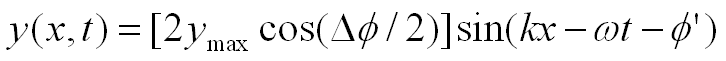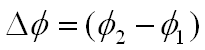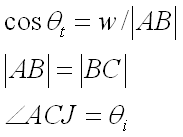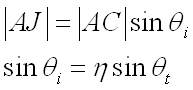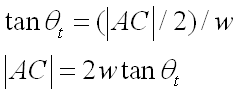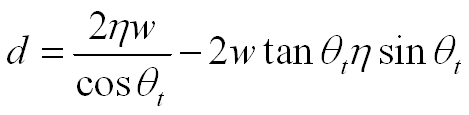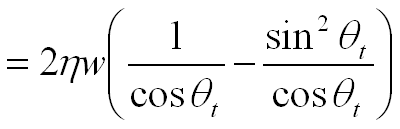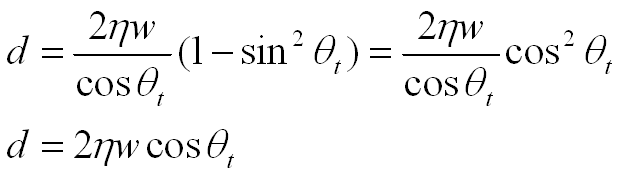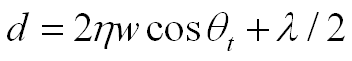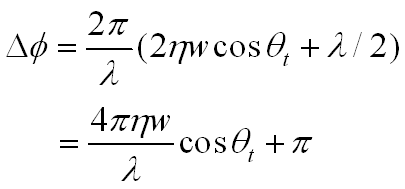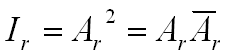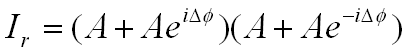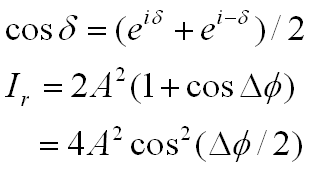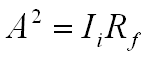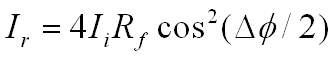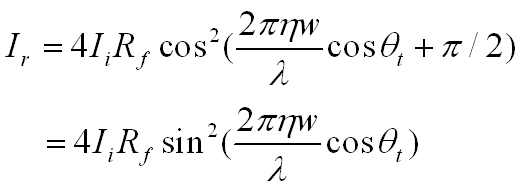Interference

by Chuck Moidel

Introduction to Light

    Light is not an easy thing to define or model.  Sometimes it exhibits the properties of a particle and other times it exhibits the properties of a wave.  This is known as the wave/particle duality of light and has been the source of much philosophizing in physics.  In computer graphics, we typically take a pragmatic course and treat light exclusively as a collection of particles (Glassner 2000).  We treat light as a particle because the particle, or photon, interpretation has simpler and more intuitive mathematics.  This translates into programs that are less computationally expensive and run faster.  This is why a majority of rendering algorithms are photon based.  The particle interpretation is usually a good choice because it covers almost all of the normal phenomena associated with light.  However, one of the most important phenomena not described by the particle model is interference.

Introduction to Interference

Waves

    Consider a transverse wave traveling along an “ideal” string in the x direction. An “ideal” string is one in which the disturbance keeps its form as it travels. This means that friction and energy dissipation are ignored. The coordinate y indicates the transverse displacement of a particular point on the string at position x and time t.

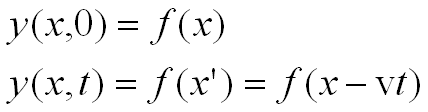
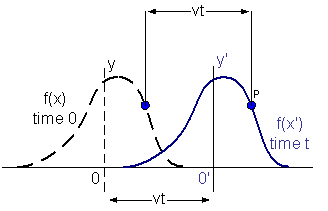
    If f is a function that describes the shape of the wave at time 0, then at time t the waveform must still be described by f. This is because we assumed that the shape does not change as the wave travels. Moving in the positive x direction at speed v for some time t, the wave will travel a distance vt. If we follow the motion of P, a particular part (or phase) of the wave, since the wave keeps its shape as it travels, the value y_p must not change. From the equation, this is only possible if the x coordinate of P increases as t increases in such as way as x-vt remains constant. This is true for any location on the waveform and for all time t.

x-vt = constant

    Now consider a sine wave traveling along an “ideal” string in the x direction. The coordinate y_max indicates the maximum displacement or amplitude of the sine curve and λ is the wavelength. The displacement y has the same value at any x as it does at x+λ, x+2λ, etc. Wavelength (in meters) equals velocity (in meters/second) times period T (in seconds).

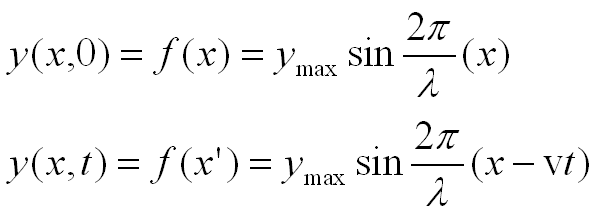
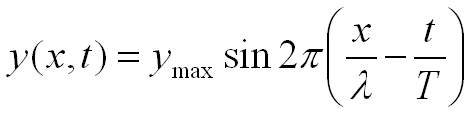
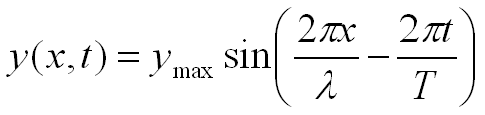
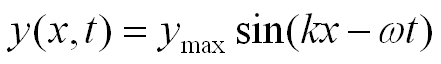
If the displacement y doesn’t equal zero at position x = 0 at time t = 0 then we need to add a phase constant.

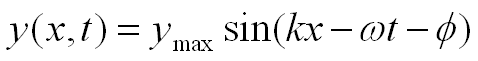
Phase shift in space:

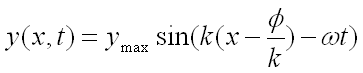
Phase shift in time:

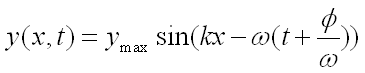
Superposition and Interference

The principle of superposition states that when several waves combine at a point, the displacement of any particle at any given time is simply the vector sum of the displacements that each individual wave acting alone would give it (Resnick 1992). For some time t and position x, y(x,t) = y1(x,t) + y2(x,t) This is why two or more waves can travel simultaneously through the same region of space independently of one another.    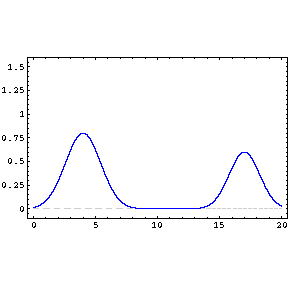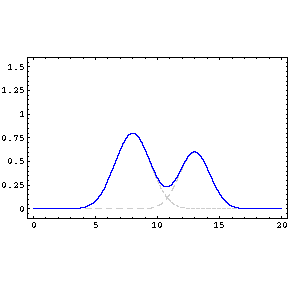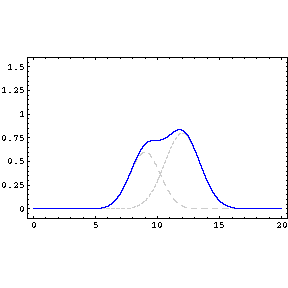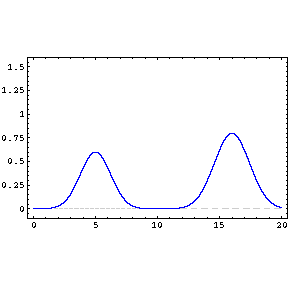When two or more waves combine at a particular point, they are said to interfere, and the phenomenon is called interference. Consider two transverse sinusoidal waves of equal amplitude and wavelength, which travel in the x direction with the same speed. If the two waves are exactly in phase, the resulting wave has twice the amplitude. This is called complete constructive interference and there is reinforcement at every point. If the two waves are only slightly out of phase, the resulting wave has close to twice the amplitude. This is called partial constructive interference. If the two waves differ in phase by π, then the resulting wave has an amplitude of 0. This is called complete deconstructive interference and there is cancellation at every point. If the two waves differ in phase by close to π, then the resulting wave has a very small amplitude. This is called partial deconstructive interference.

Given the equations for two waves y₁ and y₂:

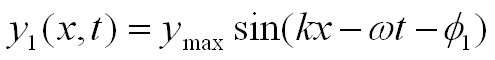
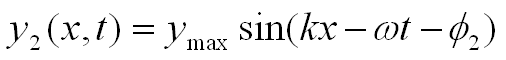
Using the principle of superposition:

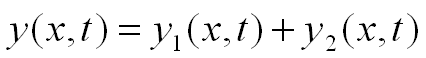
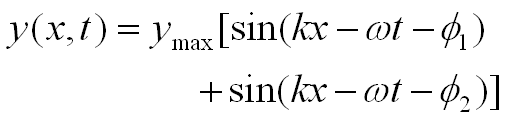
Using the trig identity for the sum of sines:

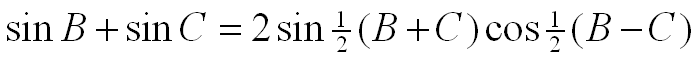
The above equation becomes:

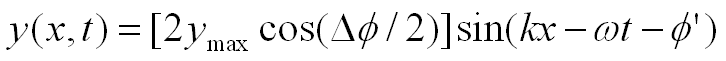
Light Interference

    Light interference is an optical phenomenon resulting from coherent superposition between lights (Sun 1999). Since light interference relies on full spectral information, a purely color based approach (such as RGB) will not suffice.  Most light interference effects observed in nature result from thin films or layers of thickness below 1 µm.  Thin film interference, or more generally, amplitude splitting interference, occurs when a wave is divided through reflection and transmission, and later recombines.  Light interference can occur on both the reflection side and the transmission side of the film.  Exiting rays that share the same direction of propagation to within a small tolerance have the potential to interfere since they having different optical path lengths.  According to the Fresnel-Arago laws, interference may be produced in the case where components of electric fields share the same plane of polarization (Gondek 1994).  However, electric fields originating from different incoherent field of natural light never produce visible interference and must be treated independently.  This means that two light rays from the same light source have the potential to interfere but two light rays from different light sources do not.

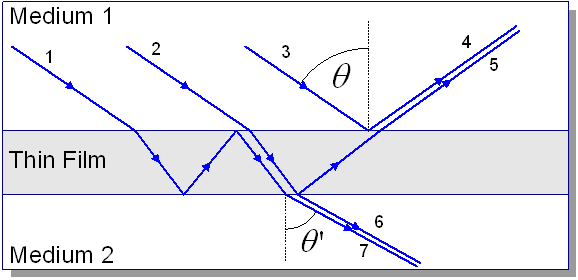
    In the image above, interference occurs between rays 4 and 5 (reflection) and between rays 6 and 7 (transmission). The propagation from 2 to 5 has an extra path inside the film compared to the propagation from 1 to 4.

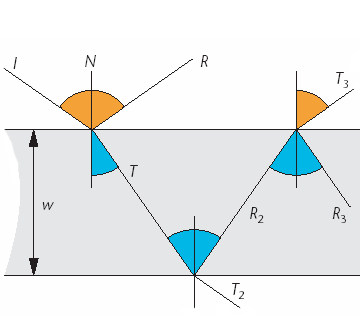
    The figure above represents a little section of soap film from a bubble. A light beam I strikes the upper surface. Some of that light is reflected in the direction R while the rest is transmitted into the film in the direction T. On the bottom of the film, some light passes into the inside of the bubble in direction T₂, while the rest is bounced upward in direction R₂. This light hits the top of the film, where some is reflected back into the film in direction R₃, while the rest comes back into the air in direction T₃. T₃ is parallel to direction R, so the light traveling on R is going to interact with the light on T₃. The resulting combined light will depend on the wavelength and phase of each constituent wave. Assume the light along I has wavelength λ, the film has thickness w, and the index of refraction of the film is η (about 1.4 for soap film). The incident angle between I and the normal N is θ_i. The light that travels through the film and exits parallel to R will be phase-shifted with respect to the light that simply reflected off the surface. The phase difference between these two waves will determine whether they reinforce or cancel each other, entirely or partly. The phase difference between the light on R and the light on T₃ consists of two components, the extra distance traveled on the longer path and the optical phase shift at the interface between the two materials.

    The extra distance can be calculated by using the equations below.  By finding the total difference in distance taken by the two beams and dividing that by the wavelength, we can determine how much of a cycle the light will pass through traveling in the film (Glassner 2000).

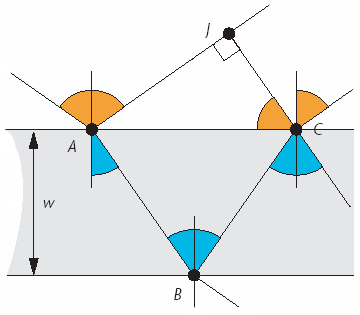
Beam 1 travels from A to J.
Beam 2 travels A to B to C
Geometric Difference = |AB|+|BC|-|AJ|

    By finding this difference and converting it to the number of radians it represents for that wavelength, we’ll get the phase difference. However, light travels more slowly in a medium that is denser than air, such as soapy water.  Because it travels more slowly, it passes through more of its cycle when going through the water than when passing through an equivalent distance of air. To model this effect, we multiply the distance traveled in the dense medium by the medium’s index of refraction. This scales up the length to the equivalent distance the wave would have covered in air in the same amount of time.

The phase difference is d=η(|AB|+|BC|)-|AJ|

Using the following equations:

We get:

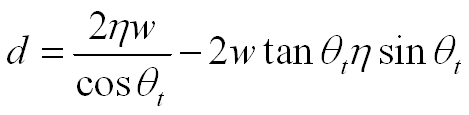
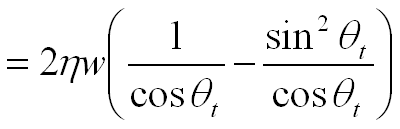
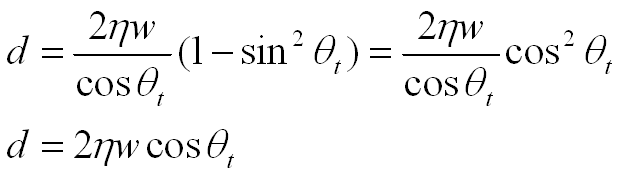
    We will now calculate the phase difference.  When light moves from one medium to a medium of higher refractive index, it undergoes a phase shift equal to half its wavelength (Glassner 2000).  One needs to add λ/2 to the difference calculated on the previous page because the light went from air to soap at point A.  To computer the phase change, Δθ, or the number of radians that this distance represents, we multiply by the number of radians in a cycle (2π) and divide by the length of one cycle (λ).

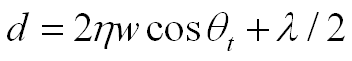
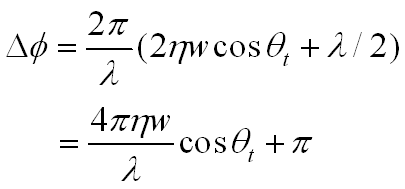
Since the intensity of light (I) is the square of the wave’s magnitude we get:

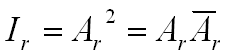
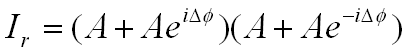
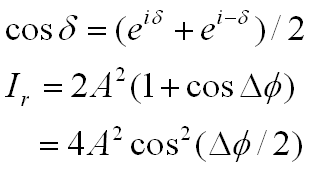
Given the reflectivity R_f from Fresnel we get:

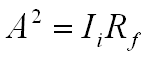
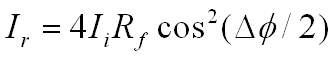
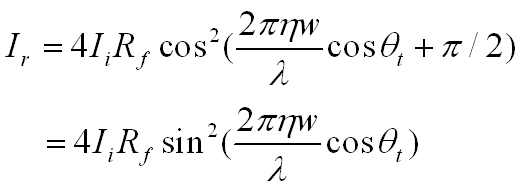
Refrences