Abandoned Mech in Forest
A CS 563
Project by
Wadii Bellamine
Intro:
The original aim of this project was to render a scene of an abandoned mechanical unit in a forest. The forest was to be filled with foliage and rocks covered with moss. The following images inspired my idea:


Figure 1: Left: Abandoned Tank in Forest. Right: Example of moss
The image on the right shows moss that looks very much like thin and thick green fur. I therefore decided to use fur modeling techniques to simulate the moss growing on rocks and on the mech. The original plan was to use L-systems to generate the vegetation, but I ended up using geometric models instead. The techniques I develop include rendering of fog and smoke, fur, bump mapping, and transparency channels (alpha channels) for textures, all of which are discussed here in detail.
Bump Mapping:
Bump mapping was used to add realism to the tree trunks, rocks, ground, and mech. The idea is to perturb the normals of the object being rendered, rather than change its geometry. This will effectively give the illusion that there is height variation on the object’s surface, because changing the normal means changing the dot product of the normal and the incident ray for lighting calculations, hence changing the amount of light that is reflected off that surface. To perform bump mapping, we need a bump map, which is typically monochrome, and represents variations in height. Consider the following simplified 9 pixel bump map:
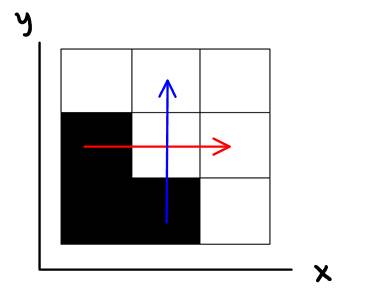
Figure 2: Simple bump map
Suppose we want to calculate the normal to the middle pixel. We can form two vectors, one in the x direction (shown in red), and one in the y direction (blue), which represent the variation in height (z axis) in the two directions. The normal to the middle pixel is then the dot product of these two vectors. If all pixels surrounding the middle pixel have the same value, then the blue vector will be (0 1 0), the red vector will be (1 0 0), and their cross product will give us the vector (0 0 -1), which will be pointing out of the screen. This would mean that no perturbation was done to the elementary normal (0 0 -1). However, if there is a variation in pixel values surrounding the middle pixel, as shown in Figure 1, the blue vector would be (0 1 -1), the red vector would be (1 0 -1), and their cross product would yield the normal (-1 -1 -1), which will be pointing like so:
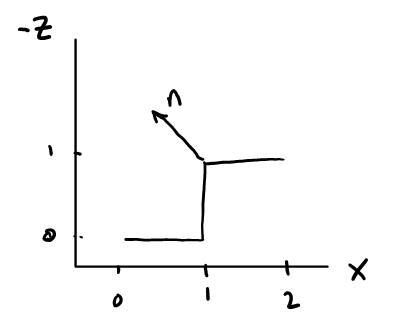
Figure 3: Looking at bump map from a different angle
This makes sense because the bump map in figure 1 has variations in height from 0 to 1, which is a step. Therefore, the normal at the middle pixel should represent the corner for this step. The following lines of code were used to find the two basis vectors (the red and blue vectors) from the bump map, and then calculate the normal by taking their cross product:
Vector3D tau(1.0,0.0,-bump_map->get_color(x+1,y).average()
+bump_map->get_color(x-1,y).average());
Vector3D beta(0.0,1.0,-bump_map->get_color(x,y+1).average()
+bump_map->get_color(x,y-1).average());
Vector3D n_object = tau^beta; //cross product gives us normal with base at (0,0,0)
There is one problem at this point: the normal we just found is in texture coordinates, whereas the normal we want needs to be in world coordinates. To transform this normal from texture to world coordinates, we use the following math:
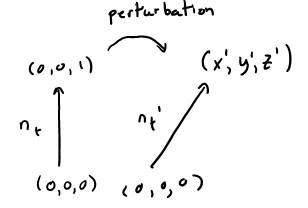
nt is the elementary normal in texture coordinates. nt’ is the perturbed normal. nt’ is the vector we obtained by taking the cross product of tau and beta. We can characterize the perturbation as a vector, and then add the perturbation vector to the normal in world coordinates, to obtain the perturbed normal in world coordinates:
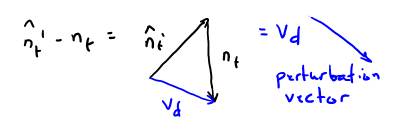
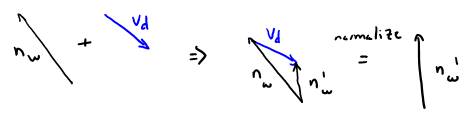
Care must be taken to normalize the perturbed normal before calculating the perturbation vector. Once we add the perturbation vector to the normal in world coordinates, we must again normalize the result to make it a unit vector.
To implement bump mapping in wxraytracer, I added a function apply_bump(sr) in the Material class. I also added a virtual function in Material which is used to assign a bump map image to any material class. Apply_bump() then obtains from sr information about the current normal at the hitpoint, the u v coordinates, and updates the normal stored in sr. Apply_bump is called from the shade function of the object that was hit. If no bump map was assigned to this object’s material, apply_bump returns sr untouched. Otherwise, it updates its normal, and all shading calculations are done with the new perturbed normal. I only added the call to apply_bump in SV_Matte, because I use bump mapping in conjuction with textures, but it can easily be incorporated in other material shade functions. The following image demonstrates my bump mapping:



Figure 4: Top left: Texture. Top Right: bump map. Bottom: Textures applied to tree trunk model
Fog:
I wanted to implement fog to see the light traversing the holes through the tree branches and leaves. That is, when rays are cast from the fog volume to the light source, and there is an obstacle in between, no light will be reaching that point, and it will be shaded with ambient lighting. To have such an effect, I use volumetric fog, and apply procedural noise to it to obtain variations in the fog and therefore have a smoke-like effect.
A volume can be thought of as a collection of particles confined in a space. These particles can be treated as microsurfaces. In order to calculate the shading of these particles, we characterize these microsurfaces with a density, a base color, and an orientation. For simple volumes, such as a fog, we can treat the particles as spheres, implying that their orientation is isotropic. We therefore only need to know the density at each point within the volume. If this density is the same throughout the volume, we obtain homogenous fog. Otherwise, we can vary density values at discrete points in space by using procedural noise functions. To obtain the color of a visible point in the volume, we use ray marching. Consider the following diagram:
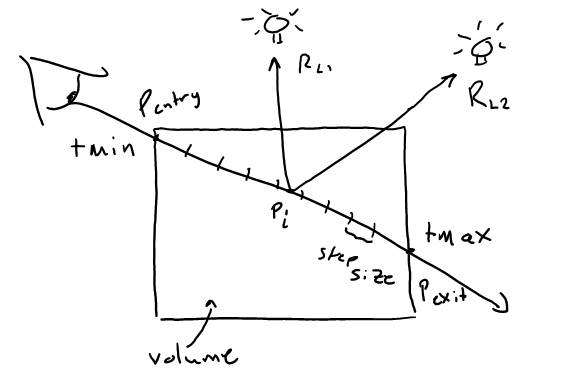
Figure 5: Volumetric ray marching process
The goal of the volumetric ray marching process is to calculate the color at Pentry. By marching through the volume, we are essentially integrating the colors of the volume at each point Pi. At the same time, we are varying the overall transparency of the volume, according to the density at each point. When tmax is reached, we have the color seen at Pentry as well as the total transparency along the ray from tmin to tmax. The final color at Pentry is obtained by scaling the resulting color by the transparency, and then adding the color at Pexit. The color at Pexit is obtained by casting a ray starting at the exit point and in the same direction as the incoming ray, and seeing what this ray hit. The following equations describe this process mathematically:
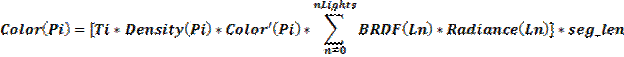
![]()
![]()
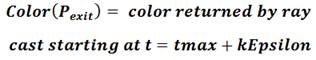
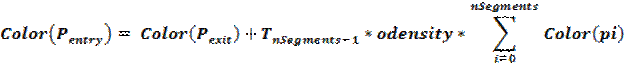
In these equations, odensity is a parameter specified by the user which defines the total transparency across the volume. This scales our transparency calculations by a desired factor so the user can adjust the overall transparency of the volume without changing the density values. Seg_len is analogous step size shown in Figure 4, and this is also a parameter defined by the user. A smaller step size means higher affinity (i. e. more precision), but also requires more processing time. The user must choose a step_size that offers the best tradeoff between sharpness and computation time. Finally, the BRDF in the first equation is set to 1 for implementing fog, because we are using sphere particles.
To implement fog, I created a new class Foggy, which is a child of Material. The shade function in foggy performs the ray marching, and also calculates the density at each point. The user can assign a Latticenoise class to the Foggy material for heterogeneous smoke. If a noise class is assigned, the density at each point is obtained by passing the current position within the volume to the noise classe’s value_fbm() function , which returns a fractal Brownian motion noise scalar value between 0 and 1. If no noise class is assigned, the value of odensity is used as the density at each point. I also introduce a sparsity parameter, which defines how far apart the particles of the volume are. This parameter represents a probability, which determines how often the density is 0. If the density is 0, the sample at that point is completely transparent, simulating an empty space. Finally, the user can define the emissive color of the volume by calling set_color, and the segment length by calling set_affinity.
The final task is assigning the fog volume to an object, and dealing with objects within this object. Consider the following diagram:
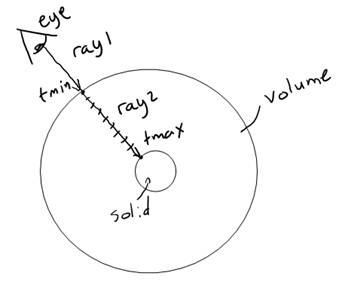
Figure 6: Solids inside a volume
Suppose, as in Figure 5, that we assigned the fog material to a sphere. When a ray (ray 1) is cast from the eye and hits the outer surface of the sphere, the tracer will call the shade function, which will be that of the foggy material. The shade function must then determine tmax before dividing up the ray into steps. The shade function must therefore cast a new ray (ray 2), starting at tmin+kEpsilon, to know what the ray will hit next. Ray 2 will return a new t value, which we will use as tmax. It will also tell us whether the ray exited the volume, or whether it hit an object within the volume. From this information, we can determine the value of Color(Pexit)shown in Figure 4.
There is, however, one more problem. Suppose we are using lights that cast shadows. Then, when a solid object is inside a volume, and casts a shadow ray towards the light source, it will intersect with the volume surface and return true, shadowing the object within the solid at all times. To avoid this, I added a condition in the sphere’s shadow hit function, which returns false (not hit) if the sphere’s material is a volume material. It knows this by looking at a flag I added in sr (isVolume).
The following image is a demo of the foggy material applied to a sphere, with a yellow color and using bicubic noise:
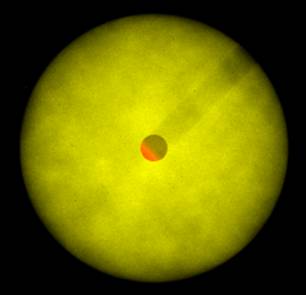
Figure 7: Foggy material applied to sphere
There is, however, a problem with this fog material: suppose we want to surround our scene with a foggy sphere. This means that every ray that we cast must march through the volume. If the scene within the volume is complex, the rendering time grows enormously. I attempted to surround my scene with a fog volume but it took more time than I had to render it. I therefore had to abandon using fog in my scene.
Texels:
The foggy material was an idea inspired from the more complex furry material which I used to simulate moss and grass. Whereas fog uses spheres to represent the particles inside the volume, the furry material uses information obtained from 3D textures, or texels. A texel, as defined by Kajiya and Kay, is a “three dimensional array of parameters approximating visual properties of a collection of microsurfaces” (Kajiya & Kay, 1989). Each cell of this array contains three parameters:
· A scalar density
· A frame bundle: normal, tangent, and binormal vectors with respect to the microsurface
· A BRDF
Since we are using hairs as our microsurfaces, our frame bundle only needs a tangent vector, which will define the orientation of the hair. Instead of storing the BRDF parameters in the texel, Kajiya and Kay suggest a way for approximating the lighting model of each hair, given that we can represent the hairs as cyclinders. The diffuse component is given as:
![]()
Where t is the tangent vector, and l is the unit vector pointing towards the light source. The specular component is given as:
![]()
Where e is the vector pointing towards the eye, and p is the exponent of the specular model as defined by the user.
If we were to render a volume with properties obtained from the cubic texel volume, we would need to define this volume, and march through it as we did with the fog volume. At each point, we would need to obtain the density and tangent vector from the texel structure, and use these along with the lighting model to calculate the color and transparency at each point. This raises the following three questions:
· How do we define our volumes so that they are attached to surfaces?
o See Defining the Furry Volume
· How do we obtain data from the texel structure if our volume is different in size, shape, and orientation from the texel structure?
o See Mapping from Object Coordinates to Texel Coordinates
· The texel structure is a 3D array, with a limited number of densities and tangents. How do we obtain more precise measurements from the texel structure ?
o See Texel Interpolation
Defining the Furry Volume
Since I will be using triangle meshes for all my objects in the scene, the fur or moss volumes need to be attached to mesh triangles. (Kajiya & Kay, 1989) only describes how to generate texel volumes for bilinear patches. (Chan, 2001) Provides code for generating texel volumes for triangular meshes. Following Chan’s approach, I added a new class called FurryMeshTriangle, which is a child of SmoothUVMeshTriangle. This will allow us to easily shade the base of the volume as a SmoothUVMeshTriangle. We must use smooth triangle because the normals at their vertices are oriented such that they are equal for all adjacent triangles. This means that we can simply extrude the base mesh triangle along these normals, and no gaps will be seen between adjacent triangle volumes:

Figure 8: Two adjacent triangles with their faces extruded along the normals
To form the new volume, given the three vertices of the triangle (b0,b1,b2), the normal at each vertex, and a height parameter:
· Calculate the tip vertices (t0,t1,t2): tip = base + height*normal
· Form 8 triangles given our 6 vertices.
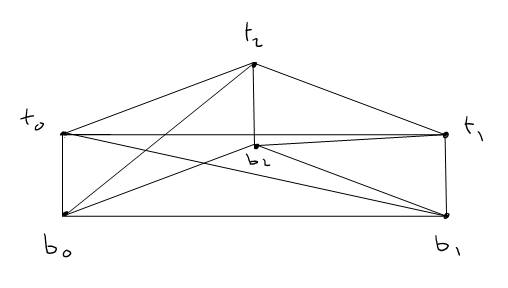
Figure 9: Forming new triangles given vertices
The furry volume is then characterized by a set of 8 triangles, one of which is the base triangle. The hit function for this object will intersect the incoming ray with each of these triangles to calculate tmin and tmax, and will store these results in the sr object, which the shade function will use to determine the extents of the volume. The hit function also sets a flag in sr, which tells the shade function whether or not the ray is exiting from the base of the triangle.
Mapping from Object Coordinates to Texel Coordinates:
Mapping of a triangular volume such as the FurryMeshTriangle to a cubic texel volume is a somewhat complex process, so it will be much clearer to start with a simpler case in order to understand at least intuitively how the mapping is done. Suppose we have a 10x10x10 texel, and a 40x40x40 cubic volume:
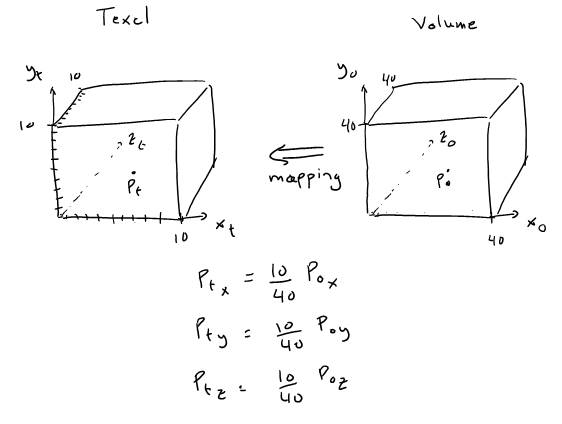
To map object coordinates to texel coordinates, we scale the object coordinates by the ratio of the dimensions of the two cubes. We can generalize this transformation for a cube in an arbitrary location with the following matrix:
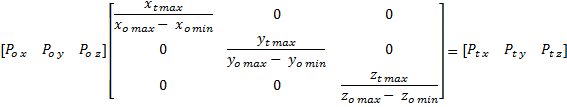
This transformation will map a cube to another cube provided that their bounding boxes are parallel to the axes of their coordinate systems. Mapping a triangular volume to the texel volume can be seen as a variation of this process, where the goal is to find the matrix which maps a point in triangular space to cubic space. (Chan, 2001) provides code for doing this, and I simply reused it.
The resulting point will then fall within the boundaries of the texel space, but it will not necessarily be three integer values. Recall that the texel volume is a 3D array, so we can only reference its cells using integer indices. This means that in order to obtain precise values for the density and tangent, we must interpolate.
Interpolating to obtain Precise Density and Tangent values:
Suppose we mapped the point from object coordinates to texel coordinates and ended up with a value such as (5.5, 4.3, 1.1). The x-coordinate falls half way between 5 and 6, the y coordinate is 70% closer to 4 than it is to 5, and the z coordinate is 90% closer to 1 than 2. In order to obtain a good approximation of density corresponding to this point, we must obtain the densities of the 4 cells adjacent to the cell (5,4,1), and take the weighted average of these densities and that of the middle cell. This process is referred to as linear interpolation in the x, y, and z directions, or tri-linear interpolation. We take the floor of the given point, calculate the residue by subtracting the floor from the original point, then lerp 4 times in x, twice in y, and once in z, to obtain the final density value. The same is done for interpolating the tangent. The code for this is found in get_density and get_tangent in the Texel class. This is the same code provided by (Chan, 2001).
Texel Self-Shadowing:
One important property of hair is the ability for individual hairs to cast shadows on other hairs in the same volume. To allow this, we need to modify the ray marching algorithm used for fog so that the shadow rays take into account the densities and tangents along the volume as they are exiting the volume:
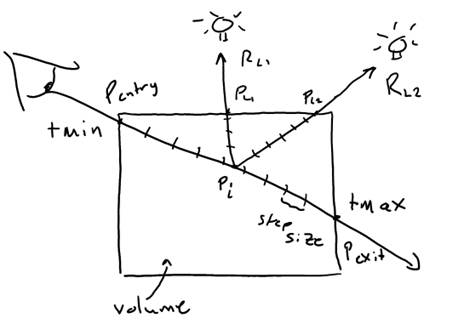
Figure 10: Texel ray marching process
Suppose we are at Pi and cast a shadow ray towards the light source L1. We must then calculate the transparency along the volume from Pi to PL1 and scale the incident radiance at Pi by this transparency. If there is a large amount of dense sub-surfaces from Pi to PL1 , then the ray marching will return a low transparency value, which will obscure most of the light coming from L1, hence simulating a shadow. The following figure shows two adjacent triangles with fur applied to them, and demonstrates the self shadowing:

Figure 11: Two triangles with fur material
There is, however, one technical issue to deal with: what if there is another texel volume between PL1 and the light source? If the shadow ray does not take this possibility into account, the fur volume surfaces separating two adjacent fur volumes end up being brighter than they should be, as shown in the following figure:

Figure 12: Problem with adjacent fur volumes
To solve this issue, we must cast a ray starting from PL1 + kEpsilon, and calculate the total transparency along the adjacent volume, if any. Since the returned transparency is a float, we need to modify the tracer to have a trace function which calls the calculate_transparency function of the given material, and returns a transparency value as a float. This means that we need to add a virtual function calculate_transparency to the Material class, which returns 0 unless it is overridden by a child class. We then over-ride this function in the Furry material class to return the appropriate transparency across the volume. Recall that the transparency of each point Pi along a volume is calculated using the following equation, where T0 is initially 1:
![]()
The transparency along the volume from tmin to tmax is then:
![]()
Equation 1
In the case of figure 9, the transparency from Pi to the exit point of the volume will use tmin = 0 and tmax = PL1. Suppose now that we have a case where the shadow ray must traverse multiple volumes, as shown below:
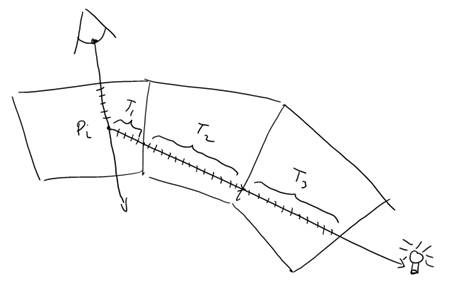
The total transparency is obtained by calculating T1, T2, and T3 using Equation 1, and summing them. This means that the calc_transparency function will call the tracer’s trace ray function, which will then recursively call calc_transparency of any other volumes until the ray exists all volumes or max depth is reached. We can represent this using the following modified equation:
![]()
Texel Coloring:
Another problem is how do we assign color to the texel? One way is to add color as a field in the texel structure. However, this means we need to define a different texel for each different color pattern, which is not very flexible or scalable. A better way is to obtain the color from the base triangle of the FurryMeshTriangle. Since we know the tangent vector at each point within the volume, and the hairs stem from the base triangle, all we need to do is cast a ray from the given point in the negative tangent direction, and obtain the color of its hit point:
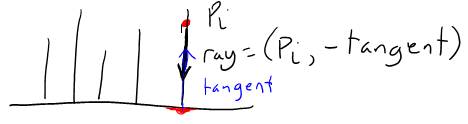
Figure 13: Calculating the color of a point in the texel
The ray will return the uv texture coordinates at the hitpoint, and we obtain the color by looking up the corresponding values in the texture that was assigned to the Furry material. The following figure demonstrates this approach:


Figure 14: Left: FurryMesh rendered using carpet texel and texture on the right
So far, we can assign a fur material to the entire object, but this is not always desired. For example, we may want to assign moss to only certain parts of a rock. To allow this, I use a density map along with the texture map. The density map returns a value which will use to scale the density at Pi, which means that if the returned value is 0, the density is 0, and therefore no fur is present at that point. Using the same technique, we cast a ray towards the base triangle, obtain the uv coordinates, and look up the pixel value in the density map, which is another parameter the user assigns to the Furry material. The following image demonstrates the same carpet using a density map (disregard the odd specular component):


Figure 15: Carpet rendering using the density map on the right
Final Notes on Texels:
We have discussed most aspects of rendering texels, but have not discussed how we define the texel structures. The Texel class provided by (Chan, 2001) reads texel description files (.desc), and generates texels according to the given density, density variation, height, height variation, optical density, and dimensions. I reused Chan’s texel class to generate the texel structures, and decided that I could create my own texel generation program after I have the texels rendering properly. By the time I got the texels to render, I had to move on to other aspects of the project, so I simply used Chan’s texel structures, as they were good enough for simulating moss.
I made it possible to assign multiple texel
structures to one Furry material, which would allow us to have different types
of fur on the same surface. However, I have not tested this feature.
The code pertaining to texels is found in Texel.cpp, Furry.cpp, and FurryMeshTriangle.cpp. Some modifications were made to ShadeRec and the Whitted tracer as discussed previously. I also made some changes to the mesh class to have a height specification, and added some code in grid.cpp to read the mesh triangles as FurryMeshTriangles.
Alpha channel:
One efficient way to render tree leaves is to apply the texture of a leaf to a plane. The problem with this is that rendering it would show the entire plane upon which the leaf texture is overlayed. To avoid using a plane that has the same shape as the leaf, we can use a transparency map which would tell the tracer where to render the plane with the texture, and when to render what is behind the plane. Consider the following leaf and its transparency map:


Figure 16: Left: Oak tree leaf. Right: Leaf's alpha channel
When the hit function of the plane that is textured with this leaf returns true, the tracer will the color of the plane’s alpha channel at the hit point. If this color is white, the tracer returns the color of the leaf by calling the plane material’s shade function. If the color is black, the tracer will cast a new ray starting from tmin+kEpsilon, and return the color of whatever this ray hits. If the value of the alpha channel is somewhere between white and black, a ray will be cast behind the plane, and the returned color will be added to the color of the plane at the hit point, scaled by the value of the alpha channel.
To integrate the alpha channel into the ray tracer, I add a new field to the RGBColor class. Each color now has r,g,b, and a components. Since the barebones ray tracer only supports ppm textures, and ppm textures are limited to 24 bit colors, I added code to the Image class in order to read bitmap files, which can have an arbitrary number of channels. The alpha channel is then integrated with the image of the texture we want to load, using an image editing software such as Photoshop, and the bitmap is exported as a 32bit color bitmap. When the bitmap is loaded in the image class, the alpha component of the RGBColor pixels is populated with reg, green, blue, and alpha fields.
To use transparency with alpha channels, I added code to the Whitted ray tracer.
Misc:
Several miscellaneous changes, and external tools where written to perform various tasks. These are described here.
UV Coordinates:
The barebones ray tracer only supports ply mesh files. Ply files require that UV coordinates be specified along with the vertices, which limits the flexibility of UV mapping. Consider the following scenario:
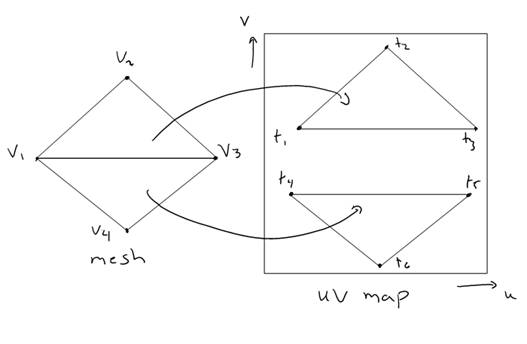
Figure 17: UV mapping
Most commercial graphic applications allow us to map each face of a mesh to a different part of the UV map, as shown in Figure 16. This means that the vertex v1 maps to both t1 and t4, and therefore has two different UV coordinates. Using PLY files, we cannot perform this type of mapping. Since I am using 3D Studio Max to edit UV maps, I need to be able to import the meshes from 3DSMax without compromising the UV mapping. 3DSMax can export meshes as obj files, which unlike ply files, assign UV coordinates to faces rather than vertices. Therefore, I added code to grid.cpp in order to read obj files and populate the mesh structure with the appropriate UV coordinates. When a new UV triangle is generated, we pass it both vertex indices and UV indices, so that the interpolate_u and interpolate_v functions in the MeshTriangle class obtain the correct UV coordinates from their respective arrays in the mesh structure.
Mech:
The mech I am using was obtained by converting .msh files from the game Rf Online into obj files. To do this, I wrote a separate program in C# which reads the .msh files, and exports them as ply files. The mech consists of 24 different meshes. However, multiple mesh pieces share the same texture. I therefore import all ply mesh pieces into 3DSMax, combine all pieces that share the same texture into a single mesh, and export them as obj files, which I then import into my raytracer. The following depicts the mech with its original texture:

Figure 18: Mech
Known Bugs:
· The fog does not render when the camera is inside of it.
· Alpha channels sometimes have the issue where the closest plane with transparency overrides all planes behind it:

· If a textured plane is placed behind another textured plane, the closer plane loses its UV mapping where the two planes overlap.
· Furry objects do not render properly if they are intersecting with another object

· Applying a furry material to meshes with disproportionate triangles causes undesired artifacts:

· Shadows cast by leaves appear as squares, the shape of the plane upon which the leaf texture is mapped:

· Furry material lighting behaves oddly when the granularity too large:

Results:

Figure 19: Close-up of rocks

Figure 20: Final Scene
Bibliography
References:
Chan, E. (2001). Texel Shader. Retrieved 03 13, 2010, from Stanford.edu:
<http://www-graphics.stanford.edu/courses/cs348b-competition/cs348b-01/fur/>
"GameDev.net - Cg Bumpmapping." GameDev.net . Web. 05 May 2010. <http://www.gamedev.net/reference/articles/article1903.asp>.
Kajiya, J. T., & Kay, L. T. (1989). Rendering Fur with Three Dimensional Textures.
Siggraph Proceedings , 271-280.
Mitchell, Dan. Photograph. Outside.danmitchell.com. Web. 5 May 2010. <http://outside.danmitchell.org/images/TreesRocksMoss20050219.jpg>.
Photograph. Pacificwrecks.com. Web. 5 May 2010. <http://www.pacificwrecks.com/tank/stuart/arawe/m3-stuart-complete.jpg>.
Textures:
"Free Concrete / Grunge Texture #1508 (dirt, Wall, Moss, Alga)." Free Textures from TextureZ.com. Web. 05 May 2010. <http://texturez.com/textures/grunge/1508>.
"Free Oak Tree Leaf Texture 03 - Oak Tree Leaf Textures - Image Gallery." 3D Artists Portal, 3d Animation and 3d Modeling Tutorials, Free Textures and Photos, 3d Jobs. Web. 05 May 2010. <http://www.3dmd.net/gallery/displayimage-1106.html>.
Models:
RF Online Game. Codemasters.