Complete by Class 8
Wiener Filtering
In this problem, we investigate the Wiener Filter discussed in class
and described in Section 5.8. Use the moon images
(moon1.img,
moon1.tif,
moon1.gif,
or
moon2.img,
moon2.tif,
moon2.gif)
Implement the following operations:
- Compute the DFT
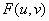 of the uncorrupted image.
of the uncorrupted image.
- Estimate the power spectrum
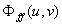 of the image.
of the image.
- Add Gaussian white noise to the image. Try
s = 10 or other value.
Call this the "corrupted" image.
- Compute the optimal Wiener filter modulation transfer function (MTF)
given by
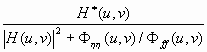
You may assume that
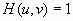 and that
and that
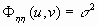 .
Use
.
Use
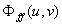 from part 2.
from part 2.
- Multiply the DFT of the corrupted image by the Wiener filter MTF to
produce the best estimate
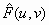 of
of
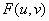 .
.
- Inverse DFT
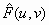 to produce the best estimate
to produce the best estimate
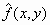 of the uncorrupted image.
of the uncorrupted image.
Display the output of each step as an image. Also display the point
spread function h(x,y) corresponding to the Wiener filter
MTF from part 4.
What to hand in
Hand in to class
- Any new programs that you have written for this
homework. Do not submit previously submitted programs.
If you made trivial modifications to a previously submitted program,
do not submit them.
- Images of each step of the Wiener filter:
- Original Image DFT
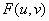 ,
,
- Original Image Power Spectrum
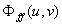 ,
,
- Noisy image (if you cannot see any noise, try increasing the noise std
dev, but beware numeric over/underflow),
- DFT of best image estimate
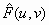 ,
,
- Best image estimate
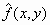 ,
and
,
and
- Wiener PSF h(x,y).
CS/ECE 545 Staff
Contents ©1997 - 2011
Norman Wittels and Michael A. Gennert
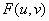 of the uncorrupted image.
of the uncorrupted image.
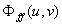 of the image.
of the image.
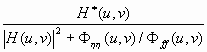
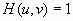 and that
and that
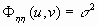 .
Use
.
Use
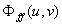 from part 2.
from part 2.
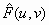 of
of
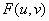 .
.
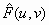 to produce the best estimate
to produce the best estimate
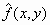 of the uncorrupted image.
of the uncorrupted image.
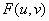 of the uncorrupted image.
of the uncorrupted image.
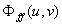 of the image.
of the image.
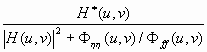
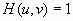 and that
and that
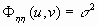 .
Use
.
Use
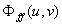 from part 2.
from part 2.
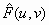 of
of
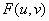 .
.
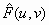 to produce the best estimate
to produce the best estimate
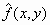 of the uncorrupted image.
of the uncorrupted image.
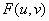 ,
,
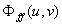 ,
,
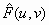 ,
,
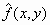 ,
and
,
and