The symbol table records information about each symbol name in a program. Historically, names were called symbols, and hence we talk about a symbol table rather than a name table. In this module, the word symbol will mean name.
It is the semantic analysis phase which creates the symbol table because it is not until the semantic analysis phase that enough information is known about a name to describe it.
Many compilers set up a table at lexical analysis time for the various variables in the program, and fill in information about the symbol later during semantic analysis when more information about the variable is known. A classic example comes from FORTRAN and Ada where the same syntax is used to refer to functions and arrays. In these languages, F(2) might refer to an element F2 of an array F or the value of function F computed using argument 2. For the lexical analyzer to make the distinction, some syntactic and semantic analysis would have to be added.
Code generation uses the symbol table to output assembler directives of the appropriate size and type.
It is important to distinguish between a symbol and an identifier since the same identifier may represent more than one name. For example, in FORTRAN, one can write:
COMMON /X/ X
F(X) = X + 1
The single identifier X represents three names:
Another example is found in block structured languages:
The picture implies that there is an outer block (or procedure) with a declaration of x and two inner blocks (or procedures) each with its own declaration of x; thus, the single identifier x again represents three different names or symbols.
Symbol Tables provide the following information:
Given an identifier, which name is it? What information is to be associated with the name?
How do we access this information>
Some symbol tables also include the keywords in the same table while others use a separate table for keywords.
Each piece of information associated with a name is called an attribute (not to be confused with the term semantic attribute from Module 6.)
Attributes are language dependent, but might include the characters in the name, the name's type, and even storage allocation information such as how many bytes the value will occupy. Often, the line number where the name is declared is recorded as well as the lines where the symbol is referenced.
If the language contains scopes, as most do (FORTRAN is an exception), then the scope is often entered into the symbol table. We will discuss a number of attributes separately beginning with the class attribute. The class of a name is an important attribute
A name in a program can represent a variable, a constant, a parameter, a record or union type, a field in a record or union, a procedure or function, a macro, an array, a label, or a file, to name just a few possibilities. These are values for a symbol's class. Of course, not all languages have all these possibilities - FORTRAN has no records - or they may be described using other terms - C uses the term union while Pascal uses the term record.
Once a name's class is known, the rest of the information may vary depending on the value of the class attribute. For example, if a name is of class variable, or constant, or parameter, to name a few, there is another attribute which records the name's type.
For a name whose class is procedure or function, there are other attributes which indicate the number of parameters, the parameters, themselves, and the result type for functions.
For a name whose class is array, other reasonable attributes are the number of dimensions and the array bounds (if known).
For a name whose class is file, other attributes might be the record size, the record type, (sequential) etc.
Again, the possible classes for a name vary with the language, as do the other attributes. (See Exercise 1.
Block Structured languages allow declarations to be nested; that is, a name can be redefined to be of a different class. A similar problem occurs when nested procedures or packages (Ada) redefine a name. The name's scope is limited to the block or procedure or function in which is is defined. In Ada, For Loop variables cause a new scope to be opened (containing only this variable).
Example 1 shows a program Main with global variables a and b, a procedure P with parameter x and a local variable a. Information about each of these names is kept in the symbol table. References to a, b, and x are made in procedure P and to its variable a.
The scope, often represented by a number, is then an attribute for the name. An alternative technique is to have a separate symbol table for each scope.
Section 7.1.1 describes how a name's other attributes may vary according to the values of its class attribute. Section 7.1.2 emphasizes the scope attribute.
Other attributes for names include the actual characters in the name's identifier, the line number in the source program where this name is declared and the line number where references occur.
Special purpose languages often have special names. Object-oriented languages, for example, may have method names, class names, and object names, in addition to the usual other classes. Scoping is particularly important in object-oriented languages because names often inherit operations and values from super classes which contain them.
Functional programming languages such as Scheme and Lisp have scoping issues which involve "binding" a name to a particular environment.
There are two main operations on symbol tables: (1) Insert (or Enter ) and (2) Lookup (or Retrieval.)
Most languages require declaration of names. When the declaration is processed, the name is inserted into the symbol table. For languages not requiring declarations, e.g., FORTRAN and SNOBOL, a name is inserted into the symbol table on its first use in the program. Each subsequent use of a name causes a symbol table lookup operation.
Given the characters of a name, searching finds the attributes associated with that name. The search time depends on the data structure used to represent the symbol table.
By External Data Structure, we mean the data structure used to represent the Symbol "Table". Internal Data structures will represent the various parts (how the names and attributes will be stored.
A symbol table makes a wonderful data structure example since the pros and cons for the various data structures can be easily explored.
Notice, first of all, that a name is entered once, but may be retrieved many times. In fact, even the enter operation may be preceded by a lookup operation to ascertain that the symbol is not already there. Thus, data structures which search rapidly are to be preferred when efficiency is an issue.
Some data structures make it easier to implement block structure information.
We will consider a number of options:
An unordered list would enter each name sequentially as it is declared. The lookup operation must then search linearly, and, thus, in the worst case, would have to look at all n entires and in the average case at half of them. Thus the search time is of order n, O(n).
There is really no good reason to have such an inefficient data structure unless it is known that the number of entries will be exceedingly small, perhaps less than a couple dozen names.
Example 2 shows an unordered list structure for the program of Example 1
Example 2 An unordered list structure
Characters Class Scope Other Attributes
Declared Referenced Other
Main Program 0 Line 1
a Variable 0 Line 2 Line 11
b Variable 0 Line 2 Line 7
P Procedure 0 Line 3 Line 11 1 param, x
x Parameter 1 Line 3
a Variable 1 Line 4 Line 6
By ordered, we mean ordered according to the characters in the name.
With an ordered array, a binary search could be done in O(log2n) time on the average, but the enter operation will take more time since elements may have to be moved. To do a binary search, however, we need to implement the ordered list as an array.
Representing the list as an ordered linked list brings us back to O(n) for the lookup operation although the enter operation would, on the average, be simpler since only pointers need to be changed rather than changing the position of each element.
Example 3 shows an ordered list. Notice that we cannot see whether this has been implemented as an array or as a linked list.
Example 3 An ordered list structure
Characters Class Scope Other Attributes Declared Referenced Other
a Variable 0 Line 2 Line 11
a Variable 1 Line 4 Line 6
b Variable 0 Line 2 Line 7
Main Program 0 Line 1
P Procedure 0 Line 3 Line 11 1 param, x
x Parameter 1 Line 3
Binary Trees combine the fast search time of an ordered array, O(log2n) on the average, with the insertion ease of alinked list. Worst case (See Exercise 2) is still O(n) for retrievals.
Example 4 shows our example for a binary tree.
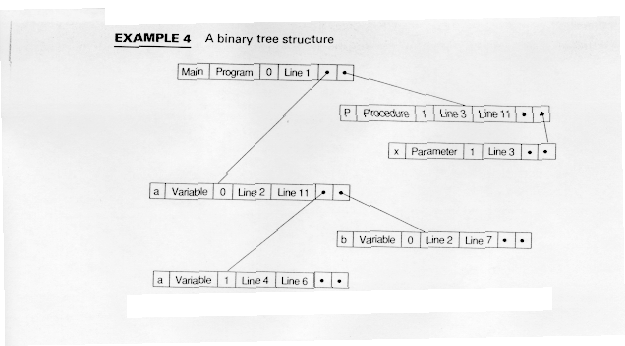In Example 4, the tree is reasonable well balanced.
Binary trees are space-efficient since they consume an amount of space proportional to the number of nodes. Since new nodes are added as leaves, scoping is difficult unless separate trees are maintained for each scope.
Outputting an alphabetized list of names is also quite easy.
If the tree is allowed to become unbalanced, searching can degrade to a linear search. Exercise 2 discusses a worst case for a binary tree implementation. Exercise 6 discusses the use of AVL trees for symbol tables.
For efficiency, hash tables are the best method. Most production-quality compilers use hashing for their symbol table structure.
Lots of hashing functions have been developed for names (See Exercise 5 ). It has been joked that the hashing table for symbol tables is irrelevant as long as it keeps the variables I, N, and X distinct!
The hashing functions consist of finding a numerical value for the identifier, perhaps some combination of the ASCII code as a number or even its bit code, and then performing some of the techniques used for hashing numbers (taking the middle values, etc.).
Example 5 creates a hash table using the formula
H(Id) = (# of first letter + # of last letter) mod 11
where # is the ASCII value of the letter.
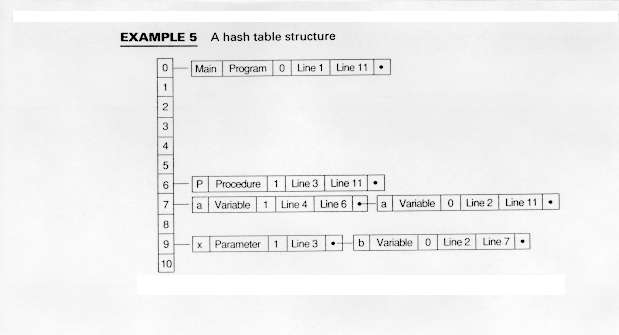
Notice in Example 5 that both instances of variable a have been hashed to the same position in the hash table and that both x and b have hashed to the same position.
If the hash function distributes the names uniformly, then hashing is very efficient - O(1) in the average case. The worst case, where all names has to the same number, has a time O(n). This case is unlikely, however.
More space is generally needed for a hash symbol table structure, so it is not as space-efficient as binary trees or list structures.
If new entries are added to the front of the linked structure, scoping is easily implemented in a single table. In fact, separate tables usually take up too much extra space.
Another data structure for a symbol table is a stack where a pointer is kept to the top of the stack for each block. In this structure, names are pushed onto the stack as they are encountered. When a block is completed, that portion of the stack and a pointer to it are moved so that the containing block's names can be completed. This is an easy structure to implement, but relatively inefficient in operation.
Combinations of the data structures are also used. Thus, we could have a hashed structured symbol table implemented as a stack.
Once the basic data structure is decided upon, we need to then decide how the names and their attribute are to be stored.
The logical view of a symbol table is a list of names, each with its own list of attributes. Each entry is thus of a variable size since the number of attributes of a name depends on its class. A data structure which allows variable lengthed entries is most space efficient, and usually a symbol "table" is not a single table, but more like a data base or a collection of data structures that work together.
Thus, the symbol table might consist of a string table where the actual characters in the name are stored, a class table where the class of the name is stored, and a name table consisting of pointers to the other two tables for each (different) name in the program.
Example 6 shows a possible symbol structure for a simple declaration. The tables shown here appear to be arrays, but they could be linked lists or some other appropriate data structure.
Here the name table has two pointers, one to A's class (Array). A pointer from the class table points to the attribute table. The attributes there indicate that the array is one-dimensional, with a lower limit of 1 and an upper limit of 100
The second pointer from the name table is to the actual character string, A.
Other attributes might include the block number or embedded procedure level where A is declared.
Symbol table information or pointers to symbol table information can be attached to the nodes of the parse tree or abstract syntax tree. Nonunique names can be replaced by dummy names (for the compiler's use). A technique for dealing with embedded declarations is to have a separate symbol table for each level and to stack the symbol tables.
In a one-pass compiler, code may be output as soon as a block is closed. Thus the symbol table structures such as a stack, which can discard the table information for nested procedures as soon as they are processed, are useful.
Attribute information is more important in a multi-pass compiler where it my be accessed by later passes.
Sophisticated languages need sophisticated compilers and hence sophisticated symbol table structures and operations. The exercises discuss a few of these more complicated structures (e.g., records) which a symbol table must handle. Other language constructs requiring artful techniques include the Pascal WITH statement, object-oriented concepts such as inheritance, the implicit declarations of languages such as FORTRAN and BASIC, the Import and Export statements of Modula-2, and polymorphism of Ada.
Compilers, and hence the symbol table, are usually written in a high-level language. Thus, the symbol table implementation is dependent on the language constructs found in this language. To be able to create a symbol table for large programs, but not waste space when creating symbol tables for small programs, requires some sort of efficient dynamic storage allocation. It has been suggested that dynamic arrays are an appropriate data structure since they avoid the "spaghetti-like" code of pointer variables and the problem of garbage collection, yet can allocate different sized objects in an efficient dynamic way.
Symbol table access can consume a major portion of compilation time. Every occurrence of an identifier in a source program requires some symbol table interaction. For a linear search this might consume as much as one-quarter of the translation time.
Symbol table actions are characterized by the fact that there are more retrievals than insertions. The entries are variable-sized depending, in particular, on the variable's class. Thus, for efficiency of time, data structures which allow fast lookup algorithms are appropriate. As is often the case, these two issues, time vs. space, may conflict.
Most compilers use either hashing or binary trees.
Since a compiler is a large software program, often maintained by people who did not write it, good programming mandates that the symbol table be written using established software engineering techniques. Regarding the symbol table as an abstract data type allows a future implementation of the symbol table to be made with minimal changes to the table's operations.
Although not discussed in this module, deletion from the symbol table is another operation which should be efficient. In a one-pass compiler, the variables in a block may be discarded upon exit from the block. In a multi-pass compiler, the "last" phase should be able to accomplish this same task.
There are other tables in a compiler. For example, literal constants may be kept in a table. Keywords may be kept in a table. If they are kept in the same table as user-defined names, they should be marked as "keywords". If a hash table is used, a hashing function which maps keywords to a different part of the table is useful.