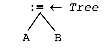6.3.6 Adding AST Routines to Recursive
Descent Parsing

An abstract syntax tree node consists of an information field and a number of pointer fields. We will show an example for the expression grammar with assignment statements added and presume a binary tree so that there are two pointer fields to a left and right child in addition to the information field.

Thus if an AST node is called Node, these three field will be denoted as Node.Info, Node.Left and Node.Right. Get(Node) will create a new emplty AST node.

The method consists of adding a parameter to each of the procedures which will carry the (partial) AST from procedure to procedure, adding on to it as appropriate.

Consider the recursive descent procedure for an assignment statement:

    {Assignment  Variable = Expression}

    PROCEDURE Assignment (Tree:AST)
    {...
     IF Next Token = Variable THEN
       Get(Node)
       Node.Info = Variable
       Node.Left = Nil
       Node.Right = Nil
       Tree = Node
     IF NextToken is "=" THEN
       Get(Node)
       Node.Info = "="
       Node.Left = Tree
       Node.Right = Nil
       Tree = Node
       Expression (Tree.Right) 
       ....
     }

Following this pseudo-code for the assignment statement:

A = B

we obtain the following abstract syntax tree, presuming the call to Expression(Tree.Right) returns a node whose information field contains B and Tree.Right is a pointer to it:

To show this, we will continue this process for Expression, Term and Factor (in outline form):

    {Expression  Term {+Term} }

    PROCEDURE Expression (Tree:AST)
    {...
     Term(Tree)
     WHILE Next Token = "+" DO
       Get(Node)
       Node.Info = "+"
       Node.Left = Tree
       Term (Tree.Right) 
       Tree = Node
       ...   
     }

    {Term  Factor {* Factor} }

    PROCEDURE Term (Tree:AST)
    {...
     Factor(Tree)
     WHILE Next Token = "*" DO
       Get(Node)
       Node.Info = "*"
       Node.Left = Tree
       Factor (Tree.Right) 
       Tree = Node
       ...   
     }

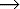    {Factor  Const | ( Expression ) }

    PROCEDURE Factor (Tree:AST)
    {...
     
     IF Next Token <> "(" THEN
       Get(Node)
       Node.Info = Token
       Node.Left = Nil
       Node.Right = Nil
       Tree = Node
       ...   
     }

Try tracing this for A = B and A = B + C * D