


The goal of Project 1 is to help you understand exactly how different search strategies work. You will implement each of nine net search algorithms. Among the searches are basic searches, heuristically informed searches, and optimal searches.
In particular, the search strategies included in this project are:
The goal of this project and homework matches the following Course Objectives:
This project consists of two parts:
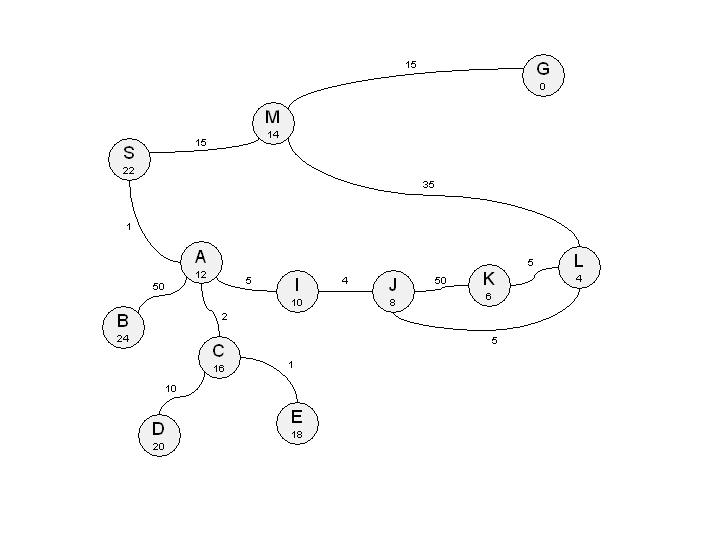
S M 15 S A 1 M G 15 A I 5 A C 2 A B 50 C E 1 C D 10 I J 4 J K 50 J L 5 K L 5 L M 35 ##### S 22 M 14 I 10 J 8 K 6 L 4 E 18 C 16 D 20 A 12 B 24
A picture of this graph is included below. Note that the (under)estimated distance of each node to the goal is included inside the node. (Special thanks to Peter Mardziel for creating this picture).
The homework assignment is the following:
The homework is due at 10 am on Friday November 07, 2003. Please hand in one HARDcopy of your group solutions to the homework assignment by the beginning of the class on Friday, Nov. 07.
Many thanks to Matt Jarvis for creating the search trees and to Peter Mardziel for generating the traces of the queues.
Depth First Expanded Queue S [<S>] A [<A,S> <M,S>] B [<B,A,S> <C,A,S> <I,A,S> <M,S>] C [<C,A,S> <I,A,S> <M,S>] D [<D,C,A,S> <E,C,A,S> <I,A,S> <M,S>] E [<E,C,A,S> <I,A,S> <M,S>] I [<I,A,S> <M,S>] J [<J,I,A,S> <M,S>] K [<K,J,I,A,S> <L,J,I,A,S> <M,S>] L [<L,K,J,I,A,S> <L,J,I,A,S> <M,S>] M [<M,L,K,J,I,A,S> <L,J,I,A,S> <M,S>] G [<G,M,L,K,J,I,A,S> <L,J,I,A,S> <M,S>] goal reached!
Breadth First Expanded Queue S [<S>] A [<A,S> <M,S>] M [<M,S> <B,A,S> <C,A,S> <I,A,S>] B [<B,A,S> <C,A,S> <I,A,S> <G,M,S> <L,M,S>] C [<C,A,S> <I,A,S> <G,M,S> <L,M,S>] I [<I,A,S> <G,M,S> <L,M,S> <D,C,A,S> <E,C,A,S>] G [<G,M,S> <L,M,S> <D,C,A,S> <E,C,A,S> <J,I,A,S>] goal reached!
Depth Limited (L=3) Expanded Queue S [<S>] A [<A,S> <M,S>] B [<B,A,S> <C,A,S> <I,A,S> <M,S>] C [<C,A,S> <I,A,S> <M,S>] I [<I,A,S> <M,S>] M [<M,S>] G [<G,M,S> <L,M,S>] goal reached!
Iterative Deepening Expanded Queue L=1 S [<S>] L=2 S [<S>] A [<A,S> <M,S>] M [<M,S>] L=3 S [<S>] A [<A,S> <M,S>] B [<B,A,S> <C,A,S> <I,A,S> <M,S>] C [<C,A,S> <I,A,S> <M,S>] I [<I,A,S> <M,S>] M [<M,S>] G [<G,M,S> <L,M,S>] goal reached!
Branch and Bound Expanded Queue S [0<S>] A [1<A,S> 15<M,S>] C [3<C,A,S> 6<I,A,S> 15<M,S> 51<B,A,S>] E [4<E,C,A,S> 6<I,A,S> 13<D,C,A,S> 15<M,S> 51<B,A,S>] I [6<I,A,S> 13<D,C,A,S> 15<M,S> 51<B,A,S>] J [10<J,I,A,S> 13<D,C,A,S> 15<M,S> 51<B,A,S>] D [13<D,C,A,S> 15<L,J,I,A,S> 15<M,S> 51<B,A,S> 60<K,J,I,A,S>] L [15<L,J,I,A,S> 15<M,S> 51<B,A,S> 60<K,J,I,A,S>] M [15<M,S> 20<K,L,J,I,A,S> 50<M,L,J,I,A,S> 51<B,A,S> 60<K,J,I,A,S>] K [20<K,L,J,I,A,S> 30<G,M,S> 50<L,M,S> 50<M,L,J,I,A,S> 51<B,A,S> 60<K,J,I,A,S>] G [30<G,M,S> 50<L,M,S> 50<M,L,J,I,A,S> 51<B,A,S> 60<K,J,I,A,S>] goal reached!
Greedy Expanded Queue S [22<S>] A [12<A,S> 14<M,S>] I [10<I,A,S> 14<M,S> 16<C,A,S> 24<B,A,S>] J [8<J,I,A,S> 14<M,S> 16<C,A,S> 24<B,A,S>] L [4<L,J,I,A,S> 6<K,J,I,A,S> 14<M,S> 16<C,A,S> 24<B,A,S>] K [6<K,J,I,A,S> 6<K,L,J,I,A,S> 14<M,S> 14<M,L,J,I,A,S> 16<C,A,S> 24<B,A,S>] L [4<L,K,J,I,A,S> 6<K,L,J,I,A,S> 14<M,S> 14<M,L,J,I,A,S> 16<C,A,S> 24<B,A,S>] K [6<K,L,J,I,A,S> 14<M,S> 14<M,L,J,I,A,S> 14<M,L,K,J,I,A,S> 16<C,A,S> 24<B,A,S>] M [14<M,S> 14<M,L,J,I,A,S> 14<M,L,K,J,I,A,S> 16<C,A,S> 24<B,A,S>] G [0<G,M,S> 4<L,M,S> 14<M,L,J,I,A,S> 14<M,L,K,J,I,A,S> 16<C,A,S> 24<B,A,S>] goal reached!
A* Expanded Queue S [22<S>] A [13<A,S> 29<M,S>] I [16<I,A,S> 19<C,A,S> 29<M,S> 75<B,A,S>] J [18<J,I,A,S> 19<C,A,S> 29<M,S> 75<B,A,S>] C [19<C,A,S> 19<L,J,I,A,S> 29<M,S> 66<K,J,I,A,S> 75<B,A,S>] L [19<L,J,I,A,S> 22<E,C,A,S> 29<M,S> 33<D,C,A,S> 66<K,J,I,A,S> 75<B,A,S>] E [22<E,C,A,S> 26<K,L,J,I,A,S> 29<M,S> 33<D,C,A,S> 75<B,A,S>] K [26<K,L,J,I,A,S> 29<M,S> 33<D,C,A,S> 75<B,A,S>] M [29<M,S> 33<D,C,A,S> 75<B,A,S>] G [30<G,M,S> 33<D,C,A,S> 54<L,M,S> 75<B,A,S>] goal reached!
Note: This version of Hill Climbing allows BACKTRACKING. Hill Climbing Expanded Queue S [22<S>] A [12<A,S> 14<M,S>] I [10<I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] J [8<J,I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] L [4<L,J,I,A,S> 6<K,J,I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] K [6<K,L,J,I,A,S> 14<M,L,J,I,A,S> 6<K,J,I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] M [14<M,L,J,I,A,S> 6<K,J,I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] G [0<G,M,L,J,I,A,S> 6<K,J,I,A,S> 16<C,A,S> 24<B,A,S> 14<M,S>] goal reached!
Beam Expanded Queue S [22<S>] A [12<A,S> 14<M,S>] M [14<M,S> 24<B,A,S> 16<C,A,S> 10<I,A,S>] G [0<G,M,S> 4<L,M,S>] goal reached!