WPI Worcester Polytechnic Institute

Computer Science Department
------------------------------------------

CS4341 Introduction to Artificial Intelligence 
Project 1 - B 2003

PROF. CAROLINA RUIZ 

PART I (Homework). DUE DATE: Friday, November 07, 10:00 am (beginning of Friday's class). 
PART I (Homework). HELP SESSION: Thursday, November 06, 1-2 pm FL A22. 
Part II (project). DUE DATE: Monday, November 10, 9:00 pm. 
BS/MS assignment. DUE DATE: Monday, November 10, 9:00 pm. 
------------------------------------------

Homework and Project Goal:

    The goal of Project 1 is to help you understand exactly how different search strategies work.  You will implement each of nine net search algorithms.  Among the searches are basic searches, heuristically informed searches, and optimal searches.

In particular, the search strategies included in this project are:

  1. Depth 1st search
  2. Breadth 1st search
  3. Depth-limited search (depth-limit = 3)
  4. Iterative deepening search (show all iterations, not just the iteration that succeeds)
  5. Basic Branch-and-bound (= Uniform cost search) with neither Estimated Distance nor Dynamic Programming
  6. Greedy search (= Best 1st search)
  7. A*
  8. Hill-climbing
  9. Beam search (w = 2)

The goal of this project and homework matches the following Course Objectives:

This project consists of two parts:

  1. Part I. A written homework assignment. Please hand in a HARDcopy of your group solutions at the beginning of class on Friday Nov. 07.
  2. Part II. An implementation project. Please submit your group solutions using the turnin system by Monday, Nov. 10 at 9:00 pm.

Part I. Homework Assignment:

Suppose that you need to find a path between S and G in the following graph. See the description of this graph input format below. 
S M 15
S A 1
M G 15
A I 5
A C 2
A B 50
C E 1
C D 10
I J 4
J K 50
J L 5
K L 5
L M 35
#####
S 22
M 14
I 10
J 8
K 6
L 4
E 18
C 16
D 20
A 12
B 24

A picture of this graph is included below. Note that the (under)estimated distance of each node to the goal is included inside the node. (Special thanks to Peter Mardziel for creating this picture).

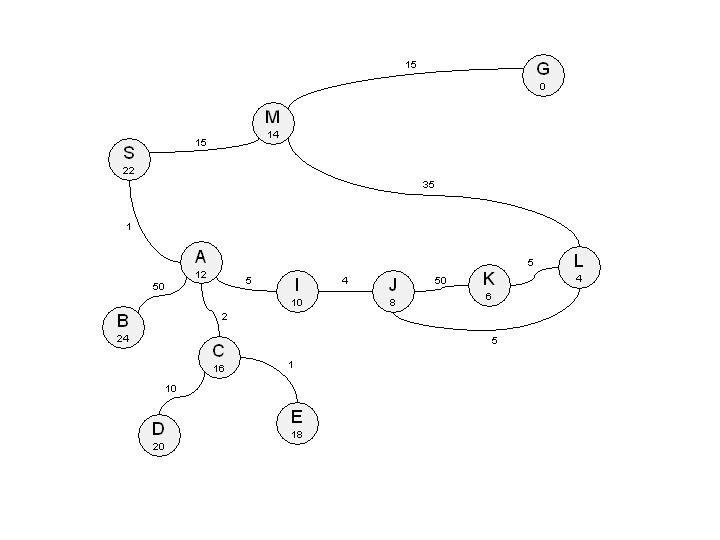
The homework assignment is the following:

Note that the homework solutions should follow exactly the same conventions as the project description below. In particular, the children of a node should be considered ordered in alphabetical order.

Homework Submission:

The homework is due at 10 am on Friday November 07, 2003.  Please hand in one HARDcopy of your group solutions to the homework assignment by the beginning of the class on Friday, Nov. 07.

Homework Grading:

Part II. Project Assignment:

Input Specifications:

    Your program must read the net to be searched from a file.  The format of the file is as follows:

The net file has two sections.  The first section describes the topology of the net and the weights (costs, distances) of the paths between nodes.  The second section provides heuristic estimates for the distances from each node to the goal node.

In the first section, each line contains all the information about one connection between two adjacent nodes.  Each of these lines has 3 fields, and each field is separated by whitespace. 

In total, the first section will contain as many lines as there are connections in the net.  You may assume that every net contains a node named 'S' and a node named 'G'.  You may also assume that the net is finite (of course).  These are the starting and goal nodes, respectively.  After the first section there will be a line separating the two sections.  This line will contain only 5 pound signs.  i.e. "#####"

The second section contains heuristic information about each node in the net (except for the goal node).  Only the heuristically informed methods should use this information.  Each line has 2 fields.

The net shown in Figure 4.1 64 of Winston's AI textbook, with the heuristic information given in Figure 4.5 is described by this file: net.txt

S A 3.0
S D 4.0
A B 4.0
B C 4.0
A D 5.0
B E 5.0
D E 2.0
F E 4.0
G F 3.0
#####
S 11.0
A 10.4
D 8.9
B 6.7
E 6.9
C 4.0
F 3.0
Please note that after F 3.0 there is a newline character. Also, note that the (under)estimate of the distance between the goal state G and itself is always 0 and hence not included in the file.

Output Specifications:

Your program should output the trace of EACH search method, in the order listed above. In particular, you should print:

When a search method backtracks past a node that has already been expanded do NOT print the name of the node again. Also, notice that you must expand a node in order to discover anything about its neighbors (children, in a search tree), but that the heuristically informed methods are not required to expand a node when they learn the node's estimated distance to the goal. The children of a node should be considered ordered in alphabetical order, that is if a node has children D, B, and F, then B will considered the 1st (or leftmost) child, D the 2nd (or middle) child, and F the last (or rightmost) child of the node. When cost/value of a path is considered (e.g. branch-and-bound, greedy search, A*, hill climbing, and beam search), and you need to decide the order of the paths in the queue according to their values (either f, g, or h values), follow the sorting procedure below:

For example, the trace of the net shown in Figure 4.1 in Winston's textbook and informed with the estimates in Figure 4.5 would produce:

(Note that for branch-and-bound 'C' is expanded even though no diagram shows this in Figure 5.2 in the textbook.  This is because it has no children, but the search still had to expand node C in order to determine that.  Also, note that Figure 4.8 in the textbook is incorrect, because S-D-E-B should never be expanded.)

        The search ends when the goal node is expanded.  Therefore if the goal is reached, it will be the last node listed.  Since some of these searches are not complete (even for finite nets!) it will be possible that the goal is not found.  In this case, the trace will end with the last node expanded before the search terminated.

Your Code:

Your program (or an accompanying script, as described in your program documentation) must accept the name of the file to read the net from.  For example, your program could be run by typing "java Search net.txt" or "search net.txt" or "runsearch net.txt"

Your solution must use a general search procedure and a general data structure (that we'll refer to in class and in this project statement as "the queue") so that each of the search strategies calls the general search procedure with a parameter specifying which search method to use.  That is, you must have a procedure that implements the following pseudo-code (adapted from Russell's and Norvig's textbook):

   function General-Search (problem, search-method) returns either a solution or failure
        queue = Make-Queue(Make-Node(problem.initial-state))
        loop do
            if queue is empty then return failure
            node =Remove-Front(queue)
            if State[node] is a solution of problem then return State[node]
            opened-nodes= Expand(node)
            queue= opened-nodes added to queue according to search-method
        end

Your procedure implementing this pseudo-code must be named General-Search as shown above.

More details about this general procedure will be given in class. For an example of how to implement each of the search strategies as a call to this general procedure, see Russell's and Norvig's online code. Although you are welcome to look at their code to guide the design of your program, you MUST submit your own original code.

Note that in order to avoid loops, you need to store not just the name of node being explored in your "queue", but also the path used to arrive to that node from the source node.

Project Submission:

Project 1 is due at 9 pm on November 10, 2003.  One (and only one) member of your group should submit the following files using the turnin program. The name of the turnin directory is proj1.

Project Grading:

Graduate Credit Problem:

This part of the assignment is INDIVIDUAL and is only required from students who are taking this course for BS/MS credit.
  1. (10 points) Construct an example of a net for which all the search methods above produce different traces. That is, no two search methods produce the same ordered list of expanded nodes. Provide your answer in the input format specified above.

  2. (10 points) Prove that A* is complete and optimal when h is an underestimate of the distance to the goal.

Graduate Credit Submission:

Each student taking this course for BS/MS should submit his/her original answers to the two problems above by email to cs4341-staff AT cs.wpi.edu in PLAIN TEXT (i.e. in an ASCII file). The submission deadline is Monday, November 10, at 9 pm.