| ID | AGE | ASTIGMATISM | TEAR-PRODUCTION-RATE | CONTACT-LENSES |
| 1. | young | no | normal | soft |
| 2. | young | yes | reduced | none |
| 3. | young | yes | normal | hard |
| 4. | pre-presbyopic | no | reduced | none |
| 5. | pre-presbyopic | no | normal | soft |
| 6. | pre-presbyopic | yes | normal | hard |
| 7. | pre-presbyopic | yes | normal | none |
| 8. | pre-presbyopic | yes | normal | none |
| 9. | presbyopic | no | reduced | none |
| 10. | presbyopic | no | normal | none |
| 11. | presbyopic | yes | reduced | none |
| 12. | presbyopic | yes | normal | hard |
The partial decision tree below shows part of the decision tree constructed by using the entropy (or disorder) based algorithm.
ASTIGMATISM
/ \
yes / \ no
/ \
TEAR-PROD-RATE ???
/ \
normal / \ reduced
/ \
AGE none
/ | \
young /PP| \ P
/ | \
hard none hard
In this problem, you are asked to finish the construction of this decision tree
following the entropy-based algorithm. In other words, you are asked to use entropy
to select the attributes that will appear in the right subtree marked with a ??? above.
| x | 1 | 1/2 | 1/3 | 2/3 | 1/4 | 3/4 | 1/5 |
| log2(x) | 0 | -1 | -1.6 | -0.6 | -2 | -0.4 | -2.3 |
For the branch astigmatism=no we measure the entropy of the remaining two predictive
attributes:
age and tear-prod-rate
AGE:
contact lenses: hard none soft
young (1/5)*[ 0 - 0 - 1*log2(1) ] = 0
pre-presb (2/5)*[ 0 - (1/2)*log2(1/2) - (1/2)*log2(1/2) ] = 0.4
presb (2/5)*[ 0 - (2/2)*log2(2/2) - 0 ] = 0
-------------
= 0.4
TEAR-PROD-RATE
contact lenses: hard none soft
normal (3/5)*[ 0 - (1/3)*log2(1/3) - (2/3)*log2(2/3)] = 0.56
reduced (2/5)*[ 0 - (2/2)*log2(2/2) -0 ] = 0
------------
= 0.56
Since the gain of the attribute age has a smaller entropy, we add this attribute to
the tree:
ASTIGMATISM
/ \
yes / \ no
/ \
TP-rate AGE
/ \ | \ \
normal / red. \ young| P| \PP
/ \ | | \
AGE none \
/ | \
young /PP| \ P
/ | \
hard none hard
For the branch(astigmatism=no and age =young) all examples have class soft and for
this branch the tree will have leaf soft.
For the branch(astigmatism=no and age =presb) all examples have class none and for
this branch the tree will have leaf none.
The Branch (astigmatism=no and age =pre-presb) doesn't give a single class so we have to
add the last available attribute TP-rate to this branch. So we will obtain the final tree:
ASTIGMATISM
/ \
yes / \ no
/ \
TP-rate AGE
/ \ | \ \
normal / red. \ young| P| \PP
/ \ | | \
AGE none soft none \
/ | \ TP-rate
young /PP| \ P / \
/ | \ reduced / \ normal
hard none hard / \
none soft
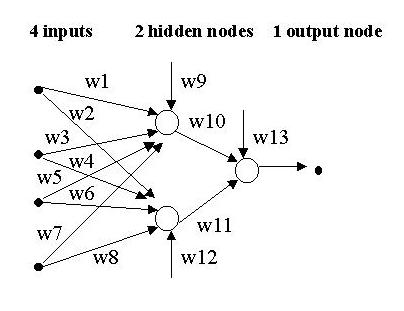
Consider the following approach to training a neural net that uses genetic algorithms instead of the error backpropagation algorithm. Assume that we are training a 2-layer, feedforward neural net with 4 inputs, 1 hidden layer with 2 hidden nodes, and one output node. The output node produces an output that is a real number between 0 and 1. Also, assume that we have a collection of n training examples to train the net, each one with a desired output, which is also a real number between 0 and 1.

An example of such an individual is:
A possible such fitness function is f( [w1, w2, ..., w12, w13] ) = n - total error where (total error) is computed as the sum of errors made by the neural net for each training instance, and n is the total number of training instances. More precisely, given an individual I, let NNI be the neural network obtained by assigning to each connection in the net the corresponding weight encoded in the individual I. Hence fitness of I = n - total error of NNI, where total error of NNI = sum over all training instances of |desired output - net's output| (A slightly modified approach is to make total error the sum of the squares of each error, i.e. total error of NNI = 1/2 * sum over all instances of (desired output - net's output)^2 ) Since both the desired and the actual outputs are values between 0 and 1, the sum over n instances will not give a number larger than n. In this manner, the highest error is n, giving a fitness of 0 (the worst fitness). The lowest error is 0 (perfect), which yields a fitness of n (the best fitness).
My initial population consists of 100 randomly generated individuals, each one being a tuple consisting of 13 randomly generated real numbers.
The selection algorithm selects 100 individuals from the current population to be included in the next generation. We first define a probability distribution over the current population (i.e. we assign a probability value to each individual in the current population in such a way that the sum of probabilities over all the individuals in the population is equal to 1). Then we do random selection with replacement using that probability distribution. We need to figure out a good way to assign probability distribution that corresponds to the chances of an individual to be selected. We choose here to use the standard selection method, but any other one described in Winston's book and covered in class (e.g. ranking method, diversity, etc.) would be fine. We already have the fitness functions that give us how well the individual performed on the training data. So, if we just divide this value by the sum of the fitness values of all the individuals in the current population, we have a probability between 0 and 1 for selection. This also directly guarantees that all the probabilities will add up to one. Then, we can simply use this probability distribution to make our selection choices.
We'll use a single cross-over points will be restricted to occur only in between two weights but not inside one weight. To determine how to combine two individuals to get two new individuals, we will split the individuals at a random point, i, using single-point crossover. All the array (tuple) positions up to i will come from the first individual, the rest of the array positions will come from the second individual. A second offspring will be generated by doing the opposite, taking all the array positions up to i from the second individual and then taking the rest from the first individual. So the result of any crossover operation would result in an individual w ith part of their weights encoded from one parent and the rest of the ANN weights from the other parent.
Mutations will be done as follows: one out of the 13 weights in an individual will be selected at random, and with a fixed probability, the selected weight will be replaced by a randomly generated real number.
There are several possible termination conditions:
(1) a maximum number of iterations,
(2) a "good-enough" individual (in this case, a threshold parameter
to determine "good-enough fitness" will be needed), or
(3) a more complex condition like the first time you have k mutations
and crossovers in a row that give no improvement to the performance
of the NN.
For the following pseudocode, let:
(1) MAX represent the maximum number of iterations
(2) Fitness_threshold represent the fitness you want to achieve
Generate the population of the initial 100 individuals P={I1, I2, ..., I100}
Evaluate each I in the Population by computing Fitness(I)
BestInd = The individual with highest fitness
Iterations = 0;
While ( Fitness(BestInd) < Fitness_threshold && Iterations < MAX )
1. Select 100 individuals at random with replacement following the
probability distribution derived from the fitness function
2. Select at random 50 pairs of individuals for crossover
3. For each pair produce two offspring and replace in the
parents with the offspring in Population
4. Mutate some percent of the Population
5. Evaluate the fitness for each new member of P
6. BestCurrent = the best fit individual from new P
7. if( Fitness(BestCurrent) > Fitness(BestInd) )
then BestInd = BestCurrent
8. Iterations ++
The best individual produced, namely BestInd in the algorithm above.
For each of the three main stages of the process, describe the stage in terms of its input/output behavior. That is, specify what the inputs and what the outputs of each of the following stages are:
Brief Description (NOT REQUIRED) Segmentation is the grouping of the pixels in the matrix into meaningful units. When segmenting a matrix of gray-scale values (most of the time) the edges of these groupings would reflect the possible boundaries of objects. There are two common methods (although many more exist): 1. Threshold: under the threshold method, the range of possible values would be split up into n equally sized slots. Each pixel would belong to the group to which its value corresponds. After processing the entire matrix, the groups are all the members of the slots. This method is sometimes bad because it can lead to pixels completely unrelated in position to be grouped just on the basis of color. 2. Assimilation: this is a similar strategy, but rather than belonging to a global group, each pixel only belongs to the pixels around it that are within a certain threshold function away from it. In this manner, similar groups are formed with similar pixels, but they are spatially isolated from similarly colored groups, leading to a better representation of the scene.
Brief Description (NOT REQUIRED)
The shape of an object can be inferred from shading, texture, and motion.
shading:
-shadows provide an understanding of the curvature of an object
-sudden shading changes represent corners or boundaries
-uniform shading in a lit scene corresponds to flat surfaces
texture:
-texture provides a perspective on the object, providing depth
-a good example is the dimples on a golf ball
motion:
-by monitoring progress as motion occurs, certain points can be
traced and a shape model developed
also:
-as an object moves, the change in the shading on the surface provides
information about the shape as well
Brief Description (NOT REQUIRED) The identification of the unknown object is done by matching the object against templates in a database. This matching process require that one identifies corresponding points points in the unknown object and in the templates. When only rotations around the y-axis are allowed, the number of templates needed is two and the the number of corresponding points needed is two. Notice that for each point we do not need a z value since in 2-D it is undetectable. Also we do not need the y coordinate since it always stays the same. So, we only need to derive a function that predicts the interpolation of the x-coordinate between the two templates we are given. The function is of the form x_need = Alpha * x1 + Beta * x2. So, we need the two points so that we can solve a system of two equations in two unknowns. The matching is done by finding the alpha and beta values for two points and then use those values of Alpha and Beta to predict the x coordinate of other control points in the unknown object based on the x coordinates of the control points in the templates. Given a small threshold for error (or mismatch), this procedure will predict which template in the database the object fits, if any at all.
Brief Description (NOT REQUIRED) During this stage, the analog signal is analyzed and split into different frequencies (or harmonics) using filters like for instance the Fourier transformation. These frequencies are used to identify basic natural language sounds, called phonemes, that appear in the signal. Identifying these phonemes may be done using a trained neural network or matching the sound (piece of input signal) against a library of known phonemes. After the phonemes are identified then complete words are constructed from the phonemes.Some difficulties present during this stage (just to mention a few are):
Brief Description (NOT REQUIRED) During this stage, the grammar of the natural language is used to determine the structure of the sentence. A grammar is a collection of rules of syntax of the language. If the sentence is syntactically ambiguous, this stage may output more than one possible syntactic structure for the sentence. A classical example of such a sentence is "Fruit flies like a banana", in which the subject can either be "Fruit" or "Fruit flies". Given a sentence and a grammar, a parsing procedure constructs one or more possible parse trees, each one representing a possible structure for the sentence. Possible complications are:
Brief Description (NOT REQUIRED) The essence of this stage is to translate the sentence into the internal knowledge representation of the computer program, so that the program can reason and use the information/knowledge encoded in the sentence. During this stage, a partial translation is made based on the parse tree(s) obtained in the previous syntactic analysis stage. As before, ambiguity is a possible complication for this stage. That is, sentences that have a unique syntactic structure but more than one possible meaning.
Brief Description (NOT REQUIRED) The purpose of this stage is to complete as much as possible the translation of the original sentence into the internal representation of the computer program. For this, the context of the sentence is used to disambiguate as much as possible the meaning of the sentence, to resolve references (e.g. "Mary bought bananas. She said they are inexpensive". In the last sentence, She="Mary" and they="bananas"). Possible complications in this stage are difficulties in understand the intentions of the speaker's message, metaphors, and semantic ambiguity.