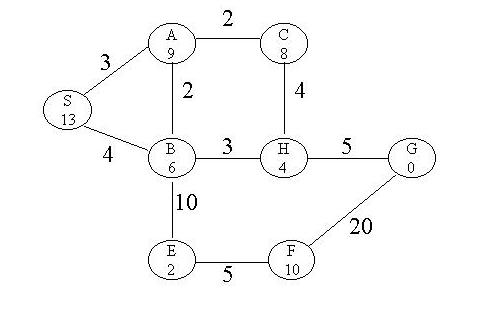

For EACH of the following search methods list the nodes in the order in which they are EXPANDED by the search method while looking for a solution. Also, show the search tree (or show the sequence of queue states instead if you prefer) as it is constructed by the search method. When everything else is equal, order the nodes in alphabetical order.
A*
Expanded Queue
S [13<S>]
B [10<B,S> 12<A,S>]
H [11<H,B,S> 12<A,S> 16<E,B,S>]
A [12<A,S> 12<G,H,B,S> 16<E,B,S> 19<C,H,B,S>]
B [11<B,A,S> 12<G,H,B,S> 13<C,A,S> 16<E,B,S>]
G [12<G,H,B,S> 12<H,B,A,S> 13<C,A,S> 16<E,B,S>]
goal reached!
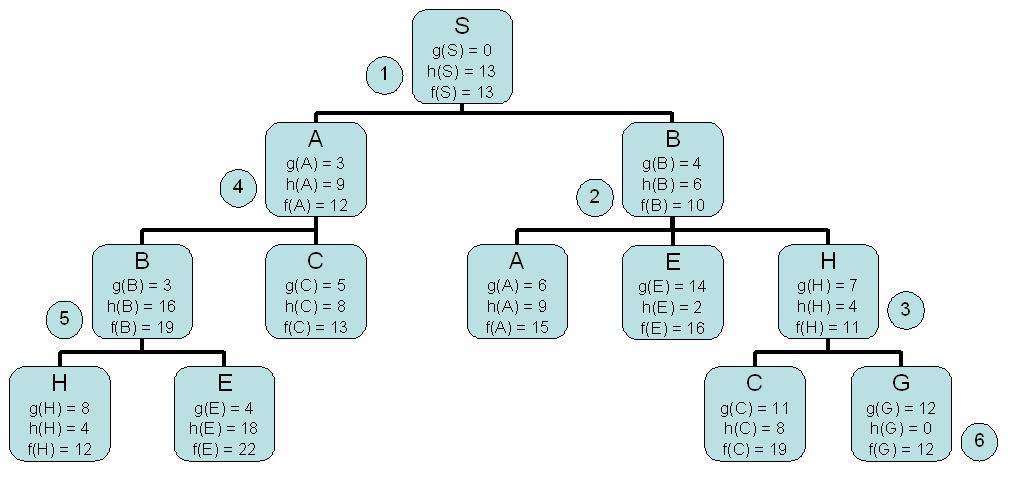
Greedy
Expanded Queue
S [13<S>]
B [6<B,S> 9<A,S>]
E [2<E,B,S> 4<H,B,S> 9<A,S> 9<A,B,S>]
H [4<H,B,S> 9<A,S> 9<A,B,S> 10<F,E,B,S>]
G [0<G,H,B,S> 8<C,H,B,S> 9<A,S> 9<A,B,S> 10<F,E,B,S>]
goal reached!
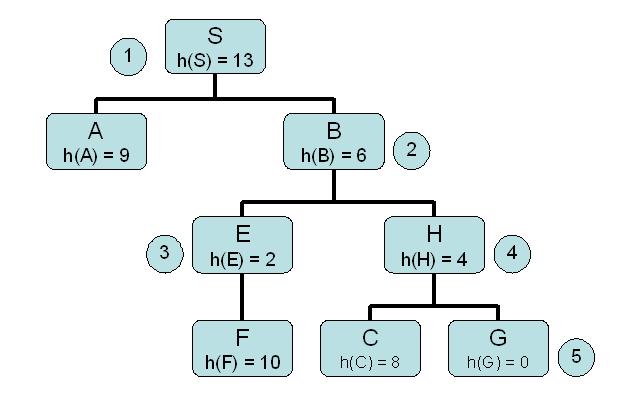
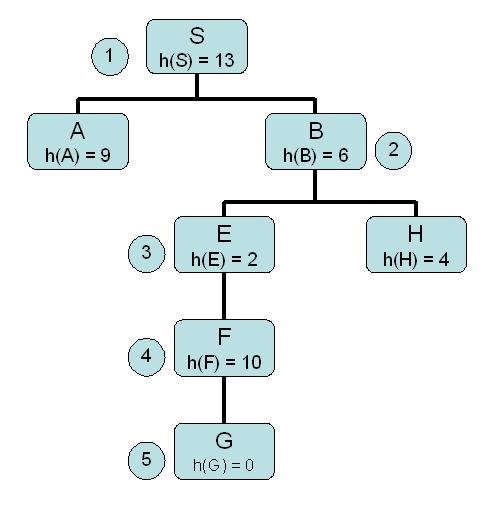
Hill Climbing
Expanded Queue
S [13<S>]
B [6<B,S> 9<A,S>]
E [2<E,B,S> 4<H,B,S> 9<A,B,S> 9<A,S>]
F [10<F,E,B,S> 4<H,B,S> 9<A,B,S> 9<A,S>]
G [0<G,F,E,B,S> 4<H,B,S> 9<A,B,S> 9<A,S>]
goal reached!
| |
------------
X | O |
------------
X | O | O
Assume also that the utility function is given by:
/
| 10, if "X" wins
utility of a terminal board configuration = | 0, if it is a draw
| -10, if "O" wins
\
Use the minimax procedure TOGETHER WITH ALPHA-BETA PRUNING to select your next move. Mark with the word "PRUNE" the nodes/branches that don't need to be evaluated (and don't expand those unnecessary branches) . Show your work on an adversarial search tree and explain your answer.
Solutions by Peter Mardziel
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
BACKWARD CHAINING:
hobbes is a tiger ?x is a tiger
|
| R4
|
hobbes has black stripes ?x has black stripes
|
| succeeds due to A1
|
hobbes is a carnivore ?x is a carnivore
|
| R3
|
hobbes eats meat ?x eats meat
|
| succeeds due to A2
|
hobbes is a mammal ?x is a mammal
|
| R1
|
hobbes gives milk ?x gives milk
succeeds due to A4
hence the working memory is updated with:
A6: hobbes is a mammal
A7: hobbes is a carnivore
A8: hobbes is a tiger
FORWARD CHAINING:
R1: hobbes gives milk ?x gives milk
succeeds due to A4
WM := WM + {A6: hobbes is a mammal} ?x is a mammal
R2: tweety has feathers ?x has feathers
|
| succeeds due to A3
|
tweety flies ?x flies
|
| succeeds due to A5
|
tweety lays eggs ?x lays eggs
fails
hence rule R2 is not triggered.
R3: hobbes eats meat ?x eats meat
|
| succeeds due to A2
|
hobbes is a mammal ?x is a mammal
succeeds due to A6
WM:= WM + {A7: hobbes is a carnivore} ?x is a carnivore
R4: hobbes has black stripes ?x has black stripes
|
| succeeds due to A1
|
hobbes is a carnivore ?x is a carnivore
succeeds due to A7
WM:= WM + {A8: hobbes is a tiger} ?x is a tiger
Applying again R1, R2, R3, R4 does not yield any new assertions
and so the forward chaining process stops.
here:
Prove the conclusion from the axioms by refutation using resolution:
!C:! happy(mary)A1: !loves(x,y) || !loves(y,x) ||happy(x)__________________________________________________ with x=mary A4:!loves(mary,y)|| !loves(y,mary) A2:loves(mary,z)__________________________________________________ with z=y A5:!loves(y,mary)A3:loves(a,mary)__________________________________________________ with y=a empty clause Since assuming that "mary is not happy" yields a contradiction in the presence of A1, A2, A3, then the statement "mary is happy" is a logical consequence of A1, A2, and A3.