


CS4341 Introduction to Artificial Intelligence
Project 2 - D 2001
By Chris Shoemaker and Carolina Ruiz
Special thanks to Mike Sao Pedro for suggesting connect4 as the game for this project
DUE DATE: Friday, Mar. 30 at 5 pm.

This project consists of designing and implementing a program that plays Connect
4. It will exemplify the minimax algorithm and alpha-beta pruning.
Connect 4 is a two player game (one of them being your computer
program). The classical game board is a 7 (horizontal) by 6 (vertical)
grid. The two players take turns dropping pieces onto the board. The player who
first gets 4 of his pieces in a row wins.
One of the players uses white pieces and the other one uses black pieces.
We will use an 7x6 board. Pieces are placed in one of the 7 columns. A
column may never have more than 6 pieces in it. We label the columns A through
G, and the rows 1 through 6.
-
Moves
The player with the white pieces moves first.
When a piece is placed in a column, it occupies the place that was
previously the lowest unoccupied place in that column. Therefore, the
first move always results in a piece occupying the lowest position in some column. The second move will either occupy the space directly above the
first piece (if the second move is in the same column as the first) or the
lowest position in some other column, (if the second move is in a different
column than the first).
One could correctly say that moves are fully determined by a sequence of columns, since the row
is always uniquely determined by the column, and the player sequence is always
alternating white and black with white beginning. However, to be more
explicit, we will describe a move as a triple: (color column row) where:
- color is either B for black or W for white,
- column is a letter from A to G,
- row is a number from 1 to 6.
- the parentheses are required.
For example the move (B D 3) means that a black piece is placed in column D,
and it occupies row 3, since rows 1 and 2 in column D are already occupied.
A game will consist of a sequence of the following actions:
- It is selected at random which player will use the white pieces and which player will use the black
pieces.
In what follows, the player that gets to use the white pieces is called player 1 and the player that gets to use
the black pieces is called player 2.
- Player 1 gets to play first.
-
After that, the players take turns moving. A move (color column row) must satisfy the following
constraints:
- Time Limit
There is a 60 second time limit for a player to make his move. (user time, not CPU time.)
- Move preconditions
- color is W if it is player 1's turn and B if it is player 2's turn.
- There is no piece at column, row.
- Every place in column, lower than row is already
occupied.
- column, row is a valid board location (A <= column
<= G, 1 <= row <= 6)
- Move postconditions
- After the move, the place at column and
row
on the board will be occupied by a color piece.
- It will be the other player's turn.
- The game ends in any of the following cases:
-
one of the players gets four of his pieces in
a row (vertically, horizontally, or diagonally). This player wins
the game, and the other loses the game.
- the board is full, but neither player can place four pieces in a row - the game
is a draw.
- a player makes an illegal move - the other player wins.
- a player fails to move within the time limit - the other player wins.
The project assignment consists of the following:
- Your group must implement a program that plays Connect 4.
- Each group needs to pick a one-word name for its program.
- Your program must use the minimax algorithm with alpha-beta pruning.
- Use a utility function (i.e. static evaluation) of your choice.
- If your minimax with alpha-beta pruning cannot expand the whole search
tree in the time allowed, your program should use a game strategy:
- Use a heuristic/evalution function of your choice (remember that the
evaluation function and the utility function must coincide on
final board configurations).
- Use a heuristic of your choice to avoid expanding the whole minimax tree.
You can choose from those covered in class (progressive deepening,
heuristic continuation (singular-extension heuristic), and tapered search)
or another one of your preference. We highly recommend using the progressive
deepening heuristic.
The better your evaluation function and your heuristic, the
better your program will play, and the better your grade in the project.
- Your program must produce only valid moves.
- Your program must verify that each of the opponent's moves is
valid, and should execute them. If the opponent's move is invalid,
your program must display the offending move, and state the error.
(e.g. space occupied, column full, lower spaces unoccupied... etc.)
- Your program must detect if the game has come to an end, and if
so, it must print a message stating who won.
- Your program must follow the specification given above so that it can
interface with other groups's programs.
- If you want, you may implement a graphical interface for your program,
that displays the configuration of the board during the game.
Such an interface is NOT required.
There are many communication methods that are far more elegant and
efficient than this one, but the intent is that this method will result in the
least elaborated code, and that it allows you to implement your program in
your choice of languages.
- Each group needs to pick a one-word name for its program.
We'll refer to that name as groupname in what follows.
- Each group must submit the code of its program and an executable (or
script) named groupname.
- A referee program, described below, will be told what two groups are going to play
and the referee will execute the programs.
- Each program will have two interface files:
groupname.in
groupname.out
-
The program will read input from groupname.in and output its moves to groupname.out
- At the beginning of the game, the file groupname.in will
contain the letter W, if the corresponding program must play
with the white pieces, and the letter B otherwise.
The referee program will take care of creating this files and making
this assignment.
- Each program must read the groupname.in file to determine which
color it will be.
- After reading its color, each program must DELETE its own
groupname.in
file, so the referee program knows that each player knows its color.
In what follows, the program that gets to use the white pieces is
called group1 and the program that gets to use the black pieces
is called group2.
- Group1 writes the first move, say (W C 1), to the file group1.out.
- Then, the referee will copy this move into group2.in
so the second program can read the move.
- After reading this
move, group2 must DELETE the group2.in file, and
before exceeding its time limit, write its move to group2.out, say (B A
1).
- The referee program will read this file and copy it
into group1.in, and the whole process is repeated until
the game is over.
- Note that a program will know that it is its turn by the presence
of a groupname.in file. After reading that file, the
program must delete it. Also, the program must CLOSE (not delete) groupname.out at the end of its turn and re-create it on its
following turn.
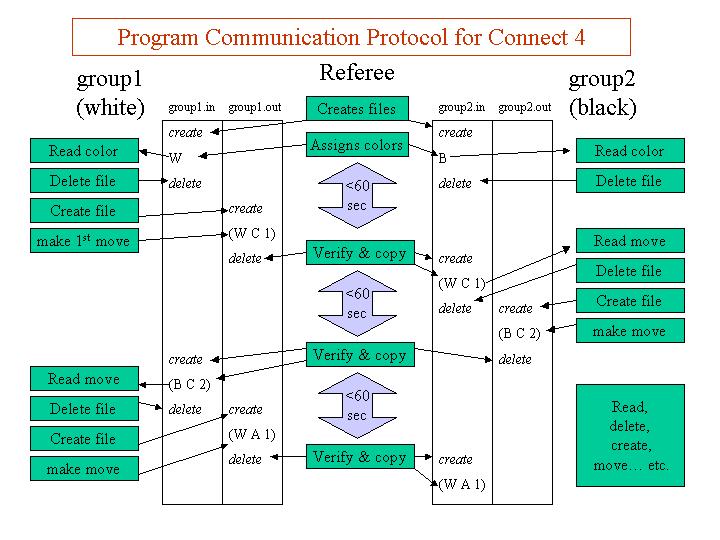
A referee program will be provided. This referee program
will be in charge of deciding which program goes first,
giving each program's turn to the other program, displaying the board
configuration, detecting illegal moves, and enforcing time
limits.
Specifically, the referee program will be in charge of:
- Assigning which program goes first, as described above.
- Displaying the board configuration after each move.
- Giving turns to each of the playing programs. By creating
the file groupname.in, the referee program is giving
the turn to groupname.
- Timing each of the players. It starts measuring the time
for groupname's move just after creating groupname.in.
If a program exceeds its time limit, the referee program
will stop the game, announcing that the offending program
has lost. (Note that a program should not time its opponent.)
- Detecting invalid moves. If the referee program
finds an invalid move, it will stop the game, announcing
that the offending program has lost.
- Ending the game when all positions on the board are
occupied, announcing a draw.
- Ending the game when one of the programs makes 4 pieces
in a row, announcing the winner.
- N.B. The time limit for the tournament will be lowered to 30 seconds.
- Your program must not consume computing resources during your opponent's
turn. In this spirit, when it is your opponent's turn, your program
should simply wait for your opponent's move. Your program may check
for the existence of the input file, at most, every 100 ms. To do
this, your process must block. In C, this will probably mean some use
of ualarm() and pause(). In Java, Thread.sleep() will do the
trick. In C++, maybe there are some convenient functions in <pthread_alloc>.
Whatever you do, you MAY NOT simply "burn time" by counting in
some tight loop in between file checks. Your process must block.
- The tournament will take place on either cpu.wpi.edu or wpi.wpi.edu.
- Both players will be executed on the same machine, and may not spawn
processes on any other machine.
MORE details have come...
- Time and Date: The tournament will be held on Sunday,
April 29th, 2001, at 2pm.
- Place: Possibly Kaven Hall computer labs, but still to be confirmed.
- Submission Date: Your group must submit your program by 12 noon,
on Sunday. No late programs will be accepted.
- Turnin Command: Use the project name "tournament" for
turning in your program with the turnin
program.
- Points: Your group can earn points in two ways.
- Successfully completing at least one game (with a win, loss, or draw)
will earn your group
a number of base points.
- Playing well will earn your group 2 points
for a win, 1 point for a draw, and 0 points for a loss.
- Tournament structure
- The tournament structure will be determined when we know how many
groups will participate.
- However, every group is guaranteed at least 3 games.
- The more games your program wins, the more games your program will
play.
- "In the end, there can be only one."
- Unless one of the finalist teams object, championship game will
take place in class on Monday.
- Groups
- Your don't have to have the same groups that you had for the
original project 2, but you do need to let us know who is in your
group.
- Below is a list of groups, and group names taken from the original
projects.
- Please email us (cs4341_ta@cs.wpi.edu)
with any additions, deletions, or name changes of group members or
groups.
| Team Members |
Group Name |
Don Asher
George Babey
Ben Dean-Kawamura
Tim Garthwaite |
Shallow Black |
Matt Morency
Dan Tana
Ben Thompson |
MRT |
Tim Sutherland
Rich Dipippo
Karin Blank
Chris Barratt |
Deep Blue |
David Mills
Yao Wen Tien
Zach Chadwick
Anthony John Andrade |
three_legged_dogs |
Gary Woo
Dominik Jatczak
Ricardo Kligman
Joel Minski |
pikao |
Sanford Freedman
Jonathan Yurek
Chuck MacAuley
Justin Lutz |
Team Bad*** |
Michael Chow
Mirek Cymer |
Player |
Michael Melson
Michael Gesner
Steve Law
John Brewer |
allyourbasearebelongtous |
Christianson, Dave
Hobbs, Ian
Schudy, Warren
Wright, Peter |
quadots |
Dan Doyle
Jared Judecki
Wendy Kogel
Steve Lesser |
Othello |
Mark Aikens
Natalie Chin
Alex Reid
Brian Faull |
BAMNit |
Along with your code, you must also submit code documentation. It must follow the Departmental Documentation Standard
(see
http://www.cs.wpi.edu/Help/documentation-standard.html). Project 2 is due at 5pm on March 30,
2001. One (and only one) member of your group must submit the following
files using the turnin
program:
- the names of the members of your group
- instructions on compiling and running your program
- the static evaluation your program uses,
- the heuristics employed,
- strategy used for minimax and alpha beta pruning,
- results:
- describe which tests you ran to try out your program.
Did you program play against human players?
Did you program play against other programs?
How did your program do during those games?
- describe the strengths and the weaknesses of
your program.
- a discussion of why the evaluation function and the heuristic are good choices.
Finding a good static evaluation function and a good heuristic
depends heavily on the experience you have with the game.
I recommend you start playing the game and getting the flavor
of what a good Connect 4 strategy is. Also, research the strategies
that other people have used for this and other games.
Lots of information can be found in the references listed in
your syllabus, the web, and magazine articles.
- Any ancillary files that your program requires, such as a script to run a
language interpreter.
Although you are welcome to look at code and systems available online to guide the
design of your program, you MUST submit your own original code.
- Connect-4: (just some of the multiple related sites are included below)
GRADUATE CREDIT PROBLEM:
- Provide DETAILED time AND space complexity analyses of using minimax to
explore ALL possible Connect4 moves starting with an empty board.
Submit a grad_project2.txt file with a text version of your answer.
![]()
![]()

