Homework Problems:
This homework consists of six problems:
Problem 1. Decision Trees (20 points)
The following table contains training examples that help predict whether
a patient is likely to have a heart attack.
| PATIENT ID | CHEST PAIN? | MALE? | SMOKES?
| EXERCISES? | HEART ATTACK?
|
| 1. | yes | yes | no | yes | yes
|
| 2. | yes | yes | yes | no | yes
|
| 3. | no | no | yes | no | yes
|
| 4. | no | yes | no | yes | no
|
| 5. | yes | no | yes | yes | yes
|
| 6. | no | yes | yes | yes | no
|
- (15 points)
Use information theory to construct a minimal decision tree that
predicts whether or not a patient is likely to have a heart attack.
SHOW EACH STEP OF THE COMPUTATION.
x 1 1/4 2/3 3/4 1/3 1/2
---------------------------------------
log_2(x) 0 -2 -0.6 -0.4 -1.6 -1
- Selecting the attribute for the root node:
Heart Attack YES NO
- Chest Pain:
- Yes: (3/6)*[ -(3/3)*log_2(3/3) - (0/3)*log_2(0/3)]
- No: (3/6)*[ -(1/3)*log_2(1/3) - (2/3)*log_2(2/3)]
- TOTAL: = 0 + 0.47 = 0.47
- Male:
- Yes: (4/6)*[ -(2/4)*log_2(2/4) - (2/4)*log_2(2/4)]
- No: (2/6)*[ -(2/2)*log_2(2/2) - (0/2)*log_2(0/2)]
- TOTAL: = 0.667 + 0 = 0.667
- Smokes:
- Yes: (4/6)*[ -(3/4)*log_2(3/4) - (1/4)*log_2(1/4)]
- No: (2/6)*[ -(1/2)*log_2(1/2) - (1/2)*log_2(1/2)]
- TOTAL: = 0.53 + 0.33 = 0.86
- Exercises:
- Yes: (4/6)*[ -(2/4)*log_2(2/4) - (2/4)*log_2(2/4)]
- No: (2/6)*[ -(2/2)*log_2(2/2) - (0/2)*log_2(0/2)]
- TOTAL: = 0.667 + 0 = 0.667
Since Chest Pain is the attribute with the lowest entropy,
it is selected as the root node:
Chest Pain
/ \
Yes / \ No
/ \
1+,2+,5+ 3+,4-,6-
HA=YES HA=?
Only the branch corresponding to Chest Pain = No needs further
processing.
- Selecting the attribute to split the branch Chest Pain = No:
Only Examples 3,4,6 need to be taken into consideration.
YES NO
- Male:
- Yes: (2/3)*[ -(0/2)*log_2(0/2) - (2/2)*log_2(2/2)]
- No: (1/3)*[ -(1/1)*log_2(1/1) - (0/1)*log_2(0/1)]
- TOTAL: = 0 + 0 = 0
Since the minimum possible entropy is 0 and Male has that
minimum possible entropy, it is selected as the best attribute
to split the branch Chest Pain=No. Note that we don't even have
to calculate the entropy of other two attributes, i.e.,
Smokes,Exercises, since they cannot possibly be better than 0.
BTW, note that the entropy of Exercises is also 0 over examples 3, 4, 6
and so it could also have been used to split this node.
Chest Pain
/ \
Yes / \ No
/ \
1+,2+,5+ 3+,4-,6-
HA=YES Male
/ \
Yes / \ No
/ \
4-,6- 3+
HA=NO HA=YES
Each branch ends in a homogeneous set of examples so the
construction of the decision tree ends here.
- (5 points)
Translate your decision tree into a collection of decision rules.
IF Chest Pain=Yes THEN Heart Attack = Yes
IF Chest Pain=No AND Male=Yes THEN Heart Attack = No
IF Chest Pain=No AND Male=No THEN Heart Attack = Yes
Problem 2. Genetic Algorithms (20 points)
Consider a genetic algorithm in which individuals
are represented a triples (x,y,z), where x, y, and z are
non-negative real numbers. Let the fitness function be given by
f(x,y,z) = (x*x) + (y*y) + z.
Complete the following table showing the probabilities
of selecting each of the individuals below according to
the different selection methods.
For the diversity method, suppose that
the first individual in the table (4,7,2) has been selected.
Compute the diversity rank for all of the remaining
individuals with respect to that first individual.
The distance between two individuals will be given by the
Euclidean distance between them, i.e.
d((x,y,z),(w,s,t)) = sqrt((x-w)^2 + (y-s)^2 + (z-t)^2),
where a^2 means a to the 2nd power, or in other words a*a.
NOTE: Following Winston's notation, below I'm calling "fitness" (in quotes)
the probability that an indiviual has of being selected under a given
selection method.
SHOW EACH STEP OF YOUR WORK.
Individuals
|
Fitness
or Quality
Rank
|
Standard
"fitness"
Rank
"fitness"
p=0.55 |
1
----
d^2 |
Diversity
rank
Diversity
+ Quality
"fitness" |
| | |
| |
| |
| (4, 7, 2) |
67 |
1 |
0.52 |
0.55 |
inf. |
5 |
0.041 |
| (2, 5, 3) |
32 |
2 |
0.25 |
0.248 |
0.111 |
4 |
0.05 |
| (0, 2, 7) |
11 |
4 |
0.085 |
0.05 |
0.0152 |
2 |
0.248 |
| (0, 4, 3) |
19 |
3 |
0.147 |
0.111 |
0.0385 |
3 |
0.111 |
| (0, 0, 0) |
0 |
5 |
0 |
0.041 |
0.0145 |
1 |
0.55 |
Calculation:
1.Quality of (4,7,2) = 4^2 + 7^2 + 2 = 67; Rank 1
Quality of (2,5,3) = 2^2 + 5^2 + 3 = 32; Rank 2
Quality of (0,2,7) = 0^2 + 2^2 + 7 = 11; Rank 4
Quality of (0,4,3) = 0^2 + 4^2 + 3 = 19; Rank 3
Quality of (0,0,0) = 0^2 + 0^2 + 0 = 0; Rank 5
2.Total = 11+ 32 + 67 + 19 + 0=129;
Standard "fitness" of (4,7,2) = 67/129 = 0.52;
Standard "fitness" of (2,5,3) = 32/129 = 0.25;
Standard "fitness" of (0,2,7) = 11/129 = 0.085;
Standard "fitness" of (0,4,3) = 19/129 = 0.147;
Standard "fitness" of (4,7,2) = 0/129 = 0;
3.Rank "fitness" of (4,7,2) = p = 0.55
Rank "fitness" of (2,5,3) = p(1-p) = 0.55*0.45 = 0.25
Rank "fitness" of (0,2,7) = p(1-p)(1-p)(1-p) = 0.05
Rank "fitness" of (0,4,3) = p(1-p)(1-p) = 0.111
Rank "fitness" of (0,0,0) = 1 - all of above = 0.041
4.1/d^2 of (4,7,2) = 1 / (0) = inf. Rank 5
1/d^2 of (2,5,3) = 1 / (4+4+1) = 0.111 Rank 4
1/d^2 of (0,2,7) = 1 / (16+25+25) = 0.0152 Rank 2
1/d^2 of (0,4,3) = 1 / (16+9+1) = 0.0385 Rank 3
1/d^2 of (0,0,0) = 1 / (16+49+4) = 0.0145 Rank 1
5.Diversity + Quality "fitness" is based on the sum of quality rank and
diversity rank, using diversity rank to break the ties.
Summed/Diversity Rank D+Q "fitness"
(4,7,2) 6/5 0.041
(2,5,3) 6/4 0.05
(0,2,7) 6/2 0.248
(0,4,3) 6/3 0.111
(0,0,0) 6/1 0.55
Problem 3. Neural Networks (20 points)
Consider the table containing heart attack data from problem 1.
Suppose that "yes" is represented by the number 1 and "no"
is represented by the number "0". The purpose of this problem
is to design a neural network and to describe the steps
that would be needed to train it so that it predicts the
whether or not a patient is likely to have a heart attack.
(Note that you don't need to run the process on a machine,
just to describe in words how the process would take place).
Answer the following question and explain your answers:
- (5 points) Neural net topology:
- How many layers would you use? Why?
Only one hidden layer in addition to the input layer and the output layer.
BTW, only one hidden layer is needed since this is a boolean function and one hidden layer is
sufficient to represent any boolean function (see Handouts).
- How many nodes per layers would you use? Why?
I'll use just two hidden units since the function seems
simple enough. In general much fewer hidden nodes than input nodes are needed.
Clearly one output node is enough to represent the binary output.
- Draw a picture of your neural net.
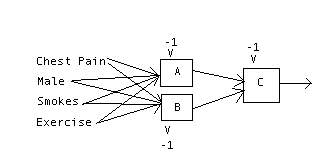
- (15 points) Training of the neural net:
- What does the error backpropagation algorithm search for?
It searches for the connections' weights that minimize the
error function (or in other words, maximize the accuracy) of the network.
- How would you initialize the weights of your net's connections?
I would select small (i.e. close to 0, positive or negative), random values.
- Carefully describe in words the steps performed by the
error backpropagation algorithm during one epoch.
The algorithm will perform the following set of steps during one epoch and will iterate them over subsequent epochs:
- Begin of Epoch:
- For each of the training examples:
- Propagate the inputs forward through the net.
- Compute the output of each node (= the sigmoid
function applied to the weighted sum of the inputs
to the node) first for the hidden layer and then for
the output layer.
- Compute the errors (i.e. the betas) associated to
each node, starting from the output layer and moving
back to the hidden layer.
- Compute and store the weight changes (i.e. the deltas)
associated with the current training example for
each of the connections in the net.
- End of Epoch
- After processing all examples, update the weight
of each connection by assigning to it the sum of that
weight's delta for each of the examples plus the current
value of the weight.
until we obtain "satisfactory weights". (See the answer
to the following question for more precise stopping
criteria).
- What stopping condition would you use?
The following are possible stopping criteria:
- When the updated weights after an iteration of the
error back propagation procedure are almost identical to
the weights before that iteration.
This is in general the best stopping criterion.
- When the output of the net is very close to the
desired one.
- When the number of iterations exceeds a pre-defined
threshold. Say the procedure has run for 20,000 iterations
and it doesn't seem to be converging.
- When the output error seems to be increasing instead
of decreasing.
- When the classification accuracy is decreasing over the validation
data (signaling overfitting).
Problem 4. Logic-based Systems (20 points)
Consider the following set of axioms:
- forall x [sum(x,0,x)]
- forall x [forall y [forall z [sum(x,y,z) -> sum(x,s(y),s(z))]]]
- forall t [exists y [sum(t,y,0)]]
And the conclusion:
- forall x [exists w [sum(x,w,s(0))]]
As usual, 0 denotes a constant; x, y, z, w, and t denote
variables; the relation sum(x,y,z) can be read as x+y=z,
and s denotes a function symbol, that can be interpreted as
the "successor" function (i.e. the increment by 1 function).
Prove the conclusion from the axioms by refutation using resolution:
- (10 points) Translate the axioms and the negation of the conclusion into clausal form.
We translate each of the axioms as follows:
The order below is very important - the steps of the transformation should
be followed in the precise order (see your textbook for that order):
- Negate the conclusion:
! forall x [exists w [sum(x,w,s(0))]] = exists x [forall w [!sum(x,w,s(0)]]
- We eliminate implications:
- forall x [sum(x,0,x)]
- forall x [forall y [forall z [!sum(x,y,z) || sum(x,s(y),s(z))]]]
- forall t [exists y [sum(t,y,0)]]
And the negation of the conclusion:
- exists x [forall w [!sum(x,w,s(0))]]
- Then we eliminate existential quantifiers:
- forall x [sum(x,0,x)]
- forall x [forall y [forall z [!sum(x,y,z) || sum(x,s(y),s(z))]]]
- forall t [sum(t,f(t),0)] WHERE f IS A NEW FUNCTION SYMBOL
NOT USED PREVIOUSLY IN THIS PROBLEM
- forall w [!sum(a,w,s(0))] WHERE a IS A NEW CONSTANT SYMBOL
NOT USED PREVIOUSLY IN THIS PROBLEM
(10 points) Apply resolution (state explicitly which substitutions are
made) until the empty clause is found.
2. !sum(x,y,z) || sum(x,s(y),s(z))
3. sum(t,f(t),0)
---------------------------------------------
5. sum(t,s(f(t)),s(0)) substituting x by t, y by f(t) and z by 0.
5. sum(t,s(f(t)),s(0))
4. !sum(a,w,s(0))
---------------------------------------------
EMPTY CLAUSE substituting t by a, and w by s(f(t)).
Problem 5. Planning (20 points)
Consider the following planning problem.
Fred is in his living room with his robot by his side
and his beer is in the kitchen. The target is to
have the beer with him in the living room.
More precisely,
- Initial State
{at(robot,living_room), at(beer,kitchen),at(fred,living_room), door_closed(kitchen,living_room)}
- Goal State
{at(robot,living_room),at(beer,living_room),at(fred,living_room), door_open(kitchen,living_room)}
- Operators
- Operator 1: open(R1,R2)
IF at(robot,R1)
door_closed(R1,R2)
ADD door_open(R1,R2)
DELETE door_closed(R1,R2)
- Operator 2: close(R1,R2)
IF at(robot,R1)
door_open(R1,R2)
ADD door_closed(R1,R2)
DELETE door_open(R1,R2)
- Operator 3: move(R1,R2)
IF at(robot,R1)
door_open(R1,R2)
ADD at(robot,R2)
DELETE at(robot,R1)
- Operator 4: carry(R1,R2,Obj)
IF door_open(R1,R2)
at(robot,R1)
at(Obj,R1)
ADD at(robot,R2)
at(Obj,R2)
DELETE at(robot,R1)
at(Obj,R1)
(20 points) Follow in detail the backward chaining algorithm described in Chapter 15 to
construct a plan to go from the initial situation
to the goal situation.
Show establishes, threatens, and before links.
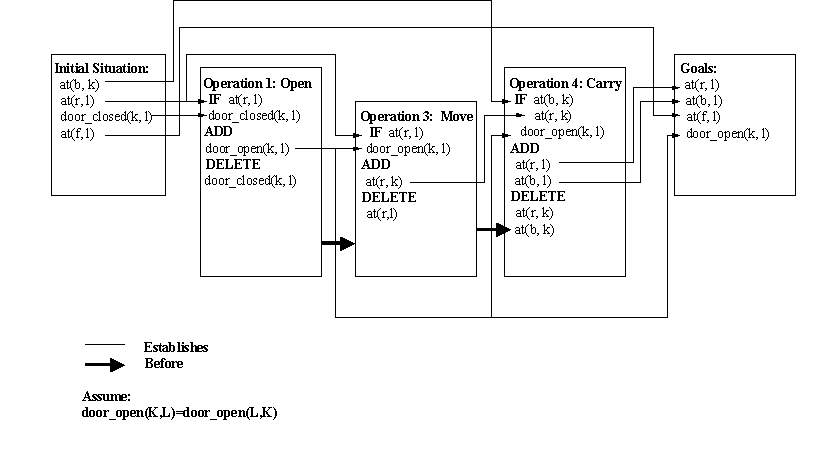
Problem 6. Machine Vision (20 points)
Solve problem 26.1 from your textbook. See pages 682-683.
Explain your answer.
Please note that there is a typo on the first table in that
problem (page 682). It should be B instead of C and C instead
of B (that is, B and C should be swapped).
By x3 = alpha*x1 + beta*x2, we can write down following equations:
x = alpha*(-1)+beta*(-1.48) -- (1)
y = alpha*3+beta*2.38 -- (2)
Solve the above two equations, we get:
alpha = x - (3x+y)*0.72 -- (3)
beta = - (3x+y)/2.06 -- (4)
For object 1, we input the its x,y value to (3) and (4), we get alpha = -1.584 , beta = 2.665.
We then test the alpha and beta on z.
However the estimated Zc = alpha*0 + beta*0.26 = 0.69 != 0, which is the actual C.
For object 2, we input the its x,y value to (3) and (4), we get alpha = 0.29 , beta = 1.451.
We then test the alpha and beta on z.
However, the estimated Zc = alpha*0 + beta*0.26 = 0.377 != 0.49, which is the actual C.
For object 3, we input the its x,y value to (3) and (4), we get alpha = -1.01, beta = 1.937
We then test the alpha and beta on z.
The estimated Zc = alpha*0 + beta*0.26 = 0.50 which is closest to the actual C, i.e., 0.49.
So Object 3 is the same model.




