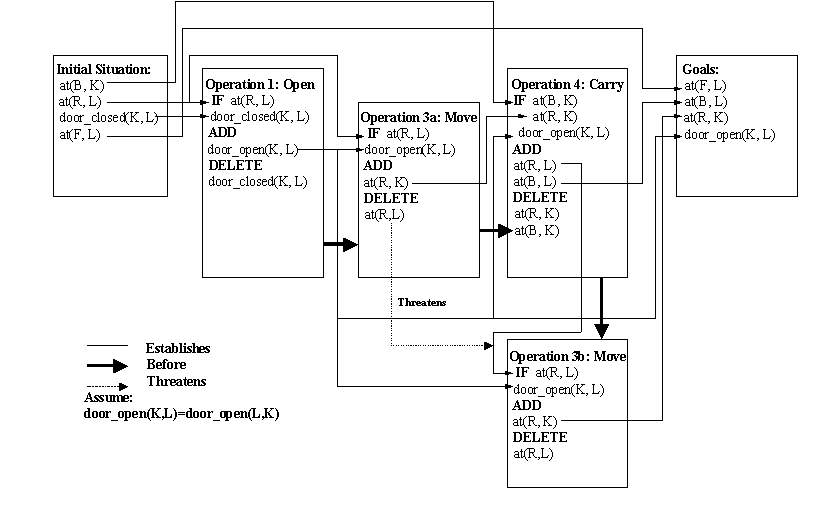
Note: In the diagram above, B stands for beer, F for Fred, R for robot, K for kitchen, L for living room. Lower case letters would have been better choice for denoting those constants.
| PATIENT ID | MAJOR OPERATION? | FAMILY AT HOME? | OLD? | SENT HOME? |
| 1. | yes | no | no | no |
| 2. | yes | no | yes | no |
| 3. | no | no | no | yes |
| 4. | no | no | yes | no |
| 5. | no | yes | yes | yes |
x 1 1/4 2/3 3/4 1/3 1/2
---------------------------------------
log_2(x) 0 -2 -0.6 -0.4 -1.6 -1
Since Major Operation is the attribute with the lowest entropy, we select it as the root node. we select it. The partially constructed tree so far is:
Major Operation
/
\
Yes
/
\ No
1-,
2-
3+, 4-, 5+
Only the branch corresponding to Major Operation = no needs further processing.
Since both attributes have the same entropy, we select either one, for example, Family at Home. The partially constructed tree so far is:
Major Operation
/
\
Yes
/
\ No
1-,
2-
\ 3+, 4-, 5+
Family at Home
/
\
Yes
/
\ No
5+
3+, 4-
Only the branch corresponding to Family at home = no needs further processing. Since Old is the last remaining attribute, we select it. The resulting tree is:
Major Operation
/
\
Yes
/
\ No
1-,
2-
\ 3+, 4-, 5+
Family at Home
/
\
Yes
/
\ No
5+
\
Old 3+, 4-
/ \
Yes / \ No
4-
3+
The fitness function is defined over these individuals
as follows:
f(b1b2b3b4b5) = b1 + b2 + b3 + b4 + b5 + AND(b1,b2,b3,b4,b5),
where AND(b1,b2,b3,b4,b5)=1 if b1=b2=b3=b4=b5=1; and AND(b1,b2,b3,b4,b5)=0 otherwise.
Answer the following questions. SHOW EACH STEP OF YOUR WORK.
Individual Fitness Standard "fitness"
or quality or probability of
being selected
00101 0+0+1+0+1+0 = 2 2/14 = .14
11101 1+1+1+0+1+0 = 4 4/14 = .29
00000 0+0+0+0+0+0 = 0 0/14 = 0
10010 1+0+0+1+0+0 = 2 2/14 = .14
11111 1+1+1+1+1+1 = 6 6/14 = .43
-------
14
(5 points) Crossover Suppose that a single crossover point will be used for crossover. This point has been chosen as the point between the 2nd and the 3rd bits (i.e. between b2 and b3). Show the two offspring that will result from crossing over the following two individuals:
PARENTS OFFSPRING:
First parent: 00.101 First offspring: 00111
Second parent: 10.111 Second offspring: 10101
(5 points) Mutation Explain how the standard mutation method is applied after selection and crossover to form the "next" generation of a population.
For each individual, a bit of the individual will be randomly selected and it will be flipped with a given "mutation rate" probability.
here:
Prove the conclusion from the axioms by refutation using resolution:
IF at(robot,R1)
door_closed(R1,R2)
ADD door_open(R1,R2)
DELETE door_closed(R1,R2)
IF at(robot,R1)
door_open(R1,R2)
ADD door_closed(R1,R2)
DELETE door_open(R1,R2)
IF at(robot,R1)
door_open(R1,R2)
ADD at(robot,R2)
DELETE at(robot,R1)
IF door_open(R1,R2)
at(robot,R1)
at(Obj,R1)
ADD at(robot,R2)
at(Obj,R2)
DELETE at(robot,R1)
at(Obj,R1)

Note: In the diagram above, B stands for beer, F for Fred, R for robot, K for kitchen, L for living room. Lower case letters would have been better choice for denoting those constants.
Two (2)
xIo = alpha * xI1 + beta * xI2
Two (2). Given that the equation above has two variables (alpha and beta) then we need two equations to be able to solve the system for those variables.
Three (3).
xIo = alphax*xI1 + betax*xI2 + gammax*xI3 + deltax
Four (4). Given that the equation above has four variables (alphax, betax, gammax, and deltax) then we need four equations to be able to solve the system for those variables.