Solutions - Exam 1 CS 4341 D01

CS4341 Introduction to Artificial Intelligence. D-2001
SOLUTIONS Exam 1 - April 5, 2001

Prof. Carolina Ruiz
Department of Computer Science
Worcester Polytechnic Institute

By Songting Chen, Greg Milette, Chris Shoemaker, and Carolina Ruiz

Instructions

Show your work
Justify your answers
Use the space provided to write your answers
Ask in case of doubt

See our grading notes for explanations on the grading codes we used.

Problem I. Search (30 points)

Suppose that you need to find a path between S and G in the following graph. The number attached to each edge in the graph represents the COST of traversing the edge.

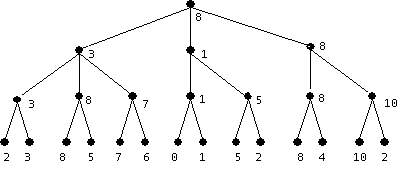
Assume also that the ESTIMATED distances to the goal are given by the following table:

Node:		S		A		C		D		F		G		H
Estimated Distance to G:		10		5		4		3		4		0		2

For EACH of the following search methods list the nodes in the order in which they are EXPANDED by the search method while looking for a solution. When everything else is equal, order the nodes in alphabetical order. As an illustration, the solution for Depth 1st search is provided below.

Depth 1st Search

List: [S, A, C, D, G]

(6 points) Breadth 1st Search

List: [S, A, F, C, F, A, G]

             S
         /        \ 
        A          F
      /   \      / | \
     C     F    A  G  H
    / \   / \      * 
   D   G G   H

(6 points) Branch-and-Bound with Dynamic Programming (= Uniform Cost Search)

List: [S, A, C, F, D, H, G]

              S
         /          \ 
      2 A            F 7
      /   \        / | \
   6 C     F      A  G  H 
    / \   10     15 12  9  
 9 D   G   x      x  x
   |  11
   G   *
  12
   x

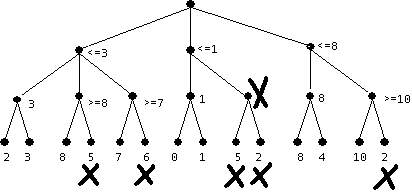
(6 points) Greedy Search (= Best 1st Search)

List: [S, F, G]

          S  10

        /   \ 

     5 A     F 4

           / | \
          A  G  H
          5  0  2
             *

(6 points) A*

List: [S, A, C, F, G]

              S
         /          \ 
      7 A            F 11
      /   \        / | \
  10 C     F      A  G  H 
    / \   14     20 12 11
   D   G   x      x  x
  12  11
       *

(6 points) Hill-climbing

List: [S, F, G]

          S  10

        /   \ 

     5 A     F 4

           / | \
          A  G  H
          5  0  2
             *

Problem II. Search (10 points)

In this problem, you are asked to construct an example showing that greedy search is not an optimal search method.

(4 points) Give an example of a net for which greedy search does not output an optimal path from S to G. Remember to provide the net, and all costs (if needed) and all estimated distances to goal.

Same net as in Example 1:

Node:		S		A		C		D		F		G		H
Estimated Distance to G:		10		5		4		3		4		0		2

(3 points) Show the order in which the nodes are expanded by the greedy search.
```
S,F,G
```
(3 points) What is the path produced by greedy search? Explain why it is not an optimal path.
```
Length of S,F,G = 12. However, there exists path S,A,C,G with length only 11.
```

Problem III. Game Playing (20 points)

Suppose you and a friend of yours are playing a board game. It is your turn to move, and the tree below represents your situation. The values of the evaluation function at the leaf nodes are shown in the tree.

(10 points) Use the minimax procedure to select your next move. Show your work on the tree below.
(10 points) Use the minimax procedure TOGETHER WITH ALPHA-BETA PRUNING to select your next move. Mark with an "X" the nodes that don't need to be evaluated. Show your work on the tree below and explain your answer.

Problem IV. Rule-Based Systems (20 points)

Consider the following set of rules for identifying animals.

R1: IF ?x gives milk THEN ?x is a mammal
R2: IF ?x has feathers AND ?x flies AND ?x lays eggs THEN ?x is a bird
R3: IF ?x eats meat AND ?x is a mammal THEN ?x is a carnivore
R4: IF ?x has black stripes AND ?x is a carnivore THEN ?x is a tiger

The working memory contains the following assertions:

A1: hobbes has black stripes
A2: hobbes eats meat
A3: tweety has feathers
A4: hobbes gives milk
A5: tweety flies

Solve the following problems. Show your work.

(10 points) Use backward chaining to determine whether or not hobbes is a tiger. Construct a tree showing the steps followed by backward chaining and show when and how the working memory is updated during the depth 1st search.


BACKWARD CHAINING:

  hobbes is a tiger                ?x is a tiger
          |
          |  R4       
          |
  hobbes has black stripes         ?x has black stripes 
          |
          |  succeeds due to A1
          |
  hobbes is a carnivore            ?x is a carnivore 
          |
          |  R3 
          |
  hobbes eats meat                 ?x eats meat 
          |
          |  succeeds due to A2
          |
  hobbes is a mammal               ?x is a mammal 
          |
          |  R1 
          |
  hobbes gives milk                ?x gives milk 

             succeeds due to A4


hence the working memory is updated with:
   A6: hobbes is a mammal  
   A7: hobbes is a carnivore
   A8: hobbes is a tiger

(10 points) Use forward chaining to derive ALL assertions that are derivable from this knowledge base (that is, from the set of rules together with the assertions in the working memory). Construct all trees showing the steps followed by forward chaining and show when and how the working memory is updated during the process.


FORWARD CHAINING:

R1:  hobbes gives milk                      ?x gives milk 
         
             succeeds due to A4
  

     WM := WM + {A6: hobbes is a mammal}    ?x is a mammal 


R2:  tweety has feathers                    ?x has feathers 
          |
          |  succeeds due to A3
          |
     tweety flies                           ?x flies 
          |
          |  succeeds due to A5
          |
     tweety lays eggs                       ?x lays eggs 

             fails


      hence rule R2 is not triggered.


R3:   hobbes eats meat                      ?x eats meat 
          |
          |  succeeds due to A2
          |
      hobbes is a mammal                    ?x is a mammal 
           
             succeeds due to A6
           

      WM:= WM + {A7: hobbes is a carnivore} ?x is a carnivore


R4:   hobbes has black stripes              ?x has black stripes 
          |
          |  succeeds due to A1
          |
      hobbes is a carnivore                 ?x is a carnivore 
          
             succeeds due to A7
          

      WM:= WM + {A8: hobbes is a tiger}     ?x is a tiger  
     

Applying again R1, R2, R3, R4 does not yield any new assertions
and so the forward chaining process stops.

Problem V. Constraint Satisfaction (20 points)

Consider the problem of scheduling a meeting that a number of people must attend. This problem can be seen as a constraint satisfaction problem under the following assumptions:

There is a variable corresponding to each of the persons who needs to attend the meeting.
Each variable (person) has unary constraints corresponding to the time availability of the person.
There are binary constraints between each two persons denoting the fact that the time scheduled for the meeting must be the same one for all persons.

Answer the following questions:

(10 points) Construct a constraint net that represents the scheduling problem described above under the following assumptions:
- The meeting has to be scheduled on a Monday or a Wednesday.
- The meeting is 1-hour long.
- The meeting must start either at 9 am or 10 am.
- Three people must attend the meeting: Bill, Ann, and Paul.
  Note then that the set of variables and their domains are:
```
    Variable      Domain
    -------------------------------------
    Bill          Mo9, Mo10, Wed9, Wed10
    Ann           Mo9, Mo10, Wed9, Wed10
    Paul          Mo9, Mo10, Wed9, Wed10

    
```
- Suppose that Bill, Ann, and Paul must attend the meeting and that their weekly time restrictions are the following:
  - Bill: Busy Mo, Wed, Fr from 9-10, 11-12, 2:30-3.
  - Ann: Busy Mo, Fr from 10:30-11:30, 3-4.
  - Paul: Busy Tu, Wed, Th from 8:30-9:30, 4-5.
Draw the complete constraint net, including full constraint matrices.
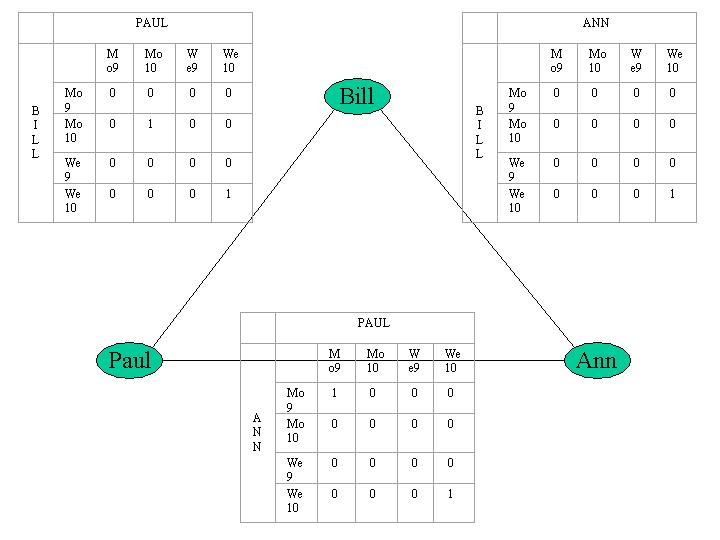
(10 points)Describe and follow in detail each of the steps of your problem solving strategy to find a convenient 1-hour slot for the meeting:
1. Arc Consistency Check
  AFTER all the constraints have been entered into the binary constraint matrices, and BEFORE the search for a solution begins, we check all the rows and columns of the binary constraint matrices for time that has all zeros, and for which the variable domain for that person still contains this time (because it was not removed by entering any of the given constraints). Such times are removed from the domain of those people, and then all binary constraint matrices for that person are updated to reflect the smaller domain. After the arc consistency checking is done, only one value remains true in each binary constraint matrix.
2. Depth First Search
  1. Selection of the 1st node
    Although all there is only value left for each binary constraint matrix, a general problem solving strategy would order the variables by how constrained they were. The depth first search would begin with an assignment of the most constrained variable.
  2. Selection of each consecutive node
    Assignments would be made for each successive node, where the selection of the next successive node would be the most constrained of the remaining variables. This would eventually lead to the discovery that the solution to the CSP is We10.

CS4341 Introduction to Artificial Intelligence. D-2001 SOLUTIONS Exam 1 - April 5, 2001

Prof. Carolina Ruiz Department of Computer Science Worcester Polytechnic Institute