CS4341 Introduction to Artificial Intelligence 
Project 3 - C 2002

By Yakov Kronrod and Carolina Ruiz
 

DUE DATE: February 17th, 2002 at 9:00 pm. 

• Project Description and Goal
• Game Description
• Project Assignment
• Program Communication
• Referee
• Tournament
• Report Submission and Due Date
• Tournament Specifications
• Other Resources
• Grading
• Summary of Help Sessions
• Graduate Credit Problem

PROJECT DESCRIPTION AND GOAL

This project consists of designing and implementing a program that plays Othello. To some this game is also known as Reversi.  It will exemplify the minimax algorithm and alpha-beta pruning. Usage of any machine learning technique (e.g. Decision Trees) along with the MinMax algorithm will earn extra credit and perhaps improve performance in the tournament.

GAME DESCRIPTION

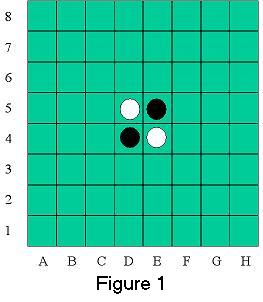
Othello is a two player game (one of them being your computer program). The classical game board is an 8 by 8 grid. At the start of the game there are four pieces in the center of the grid. White in the top-left and bottom-right. Black in the top-right and bottom-left. (See Figure 1 for initial configuration) Players take turns placing pieces on the board until the board is full. The object is to catch opponent's pieces between two of your pieces to flip them to your color. At the end of the game, whoever has the most pieces on the board wins. 

• Pieces

One of the players uses white pieces and the other one uses black pieces.

• Board

We will use an 8x8 board. We will label the the board as in Figures 1-3: columns A through H (left to right), and the rows 1 through 8 (bottom to top). 

• Moves

  The player with the white piece moves first.

    There are two types of legal moves. First are those which trap at least one opponent piece between pre-existing pieces of your color on the board and the currently placed piece. This trapping could be horizontal, vertical, or diagonal. The other legal move is a PASS. This move can only be taken when there are no trapping legal moves available for the player to take. See links at the bottom for game downloads and online play.

    It is true that moves alternate between black and white, but to be explicit, we will describe a move as a triple: (color column row) where:

  • color is either B for black or W for white,
  • column is a letter from A to H, or P for passing
  • row is a number from 1 to 8, (doesn't matter which number if column=P)
  • the parentheses are required.
  NOTE: Executing a PASS when there are other moves is considered an illegal move. In the tournament, this would automatically cause a loss.

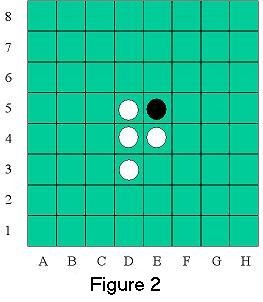
  For example, a possible first move of the game is (W D 3), meaning that a white piece is placed in column D (the fourth from the left), and it occupies row 3 (the third from the bottom). This would result in the black piece at (D,4) being converted to a white piece (see Figure 2). It would then be player 2's turn. A possible move for Black would be (B C 3), placing a black piece in column C, row 3. This results in the white piece at (D,4) being converted to a black piece (see Figure 3).

• Game Rules

A game will consist of a sequence of the following actions:

1. It is selected at random which player will use the white pieces and which player will use the black pieces. In what follows, the player that gets to use the white pieces is called player 1 and the player that gets to use the black pieces is called player 2.

2. Player 1 gets to play first.

3. After that, the players take turns moving.  A move (color column row) must satisfy the following constraints:
   • Time Limit There is a 60 second time limit for a player to make his move. (user time, not CPU time.)
   • Move preconditions (if not passing)
     1. color is W if it is player 1's turn and B if it is player 2's turn.
     2. There is no piece at column, row.
     3. column, row is a valid board location (A <= column <= H, 1 <= row <= 8)
     4. There is a sequence of opponent pieces followed by your piece starting from column, row in at least one of eight directions. If not, the turn is lost and the other player goes again.
   • Move postconditions (if not passing)
     1. After the move, the place at column and row on the board will be occupied by a color piece.
     2. For each of eight directions (up, up-right, right, right-down, down, down-left, left, left-up) any sequence of opponent pieces followed by your piece starting at column, row is converted to a color piece.
     3. It will be the other player's turn.
   • Move preconditions (if column = P)
     1. There is no open (col,row) with a necessary sequence of opponent pieces followed by your piece starting there.
   • Move postconditions (if column = P)
     1. The board configuration remains unchanged
     2. It will be the other player's turn.

4. The game ends in any of the following cases:
   1. The board is full. The player with the most pieces wins the game, and the other loses the game. If the number of pieces is equal, then the game is a draw.
   2. neither player can make a legal move, the player with the most pieces wins.
   3. a player makes an illegal move - the other player wins.
   4. a player fails to move within the time limit - the other player wins.

PROJECT ASSIGNMENT

1. Your group must implement a program that plays Othello.
2. Each group needs to pick a one-word name for its program.
3. Your program must use the minimax algorithm with alpha-beta pruning.
• Use a utility function (i.e. static evaluation) of your choice.
4. If your minimax with alpha-beta pruning cannot expand the whole search tree in the time allowed, your program should use a game strategy:
   • Use a heuristic/evalution function of your choice (remember that the evaluation function and the utility function must coincide on final board configurations). You are encouraged to use machine learning techniques here to obtain a good heuristic function.
   • Use a heuristic of your choice to avoid expanding the whole minimax tree. You can choose from those covered in class (progressive deepening, heuristic continuation (singular-extension heuristic), and tapered search) or another one of your preference. We highly recommend using the progressive deepening heuristic.
   The better your evaluation function and your heuristic, the better your program will play, and the better your grade in the project.
5. Your program must produce only valid moves.
6. Your program must verify that each of the opponent's moves is valid, and should execute them.  If the opponent's move is invalid, your program must display the offending move, and state the error.  (e.g. space occupied, no trap) 
7. Your program must detect if the game has come to an end, and if so, it must print a message stating who won.
8. Your program must follow the specification given above so that it can interface with other groups's programs.
9. If you want, you may implement a graphical interface for your program, that displays the configuration of the board during the game. Such an interface is NOT required.
10. Use of a machine learning technique in addition to minimax with alpha-beta prunning is completely optional but very much encouraged.

PROGRAM COMMUNICATION IN THE TOURNAMENT

There are many communication methods that are far more elegant and efficient than this one, but the intent is that this method will result in the least elaborated code, and that it allows you to implement your program in your choice of languages. The debugging is also simple since you can control the contents of these files with the use of any text editor.

1. Each group needs to pick a one-word name for its program. We'll refer to that name as groupname in what follows.
2. Each group must submit the code of its program and an executable (or script) named groupname.
3. A referee program, described below, will be told what two groups are going to play and the referee will execute the programs.
4. Each program will have two interface files:
      groupname.in
      groupname.out

5. The program will read input from groupname.in and output its moves to groupname.out

6. At the beginning of the game, the file groupname.in will contain the letter W, if the corresponding program must play with the white pieces, and the letter B otherwise. The referee program will take care of creating this files and making this assignment.
7. Each program must read the groupname.in file to determine which color it will be.
8. After reading its color, each program must DELETE its own groupname.in file, so the referee program knows that each player knows its color. In what follows, the program that gets to use the white pieces is called group1 and the program that gets to use the black pieces is called group2.
9. Group1 writes the first move, say (W D 3), to the file group1.out.
10. Then, the referee will copy this move into group2.in so the second program can read the move.
11. After reading this move, group2 must DELETE the group2.in file, and before exceeding its time limit, write its move to group2.out, say (B C 3).
12. The referee program will read this file and copy it into group1.in, and the whole process is repeated until the game is over.
13. Note that a program will know that it is its turn by the presence of a groupname.in file. After reading that file, the program must delete it. Also, the program must CLOSE (not delete) groupname.out at the end of its turn and re-create it on its following turn.

REFEREE

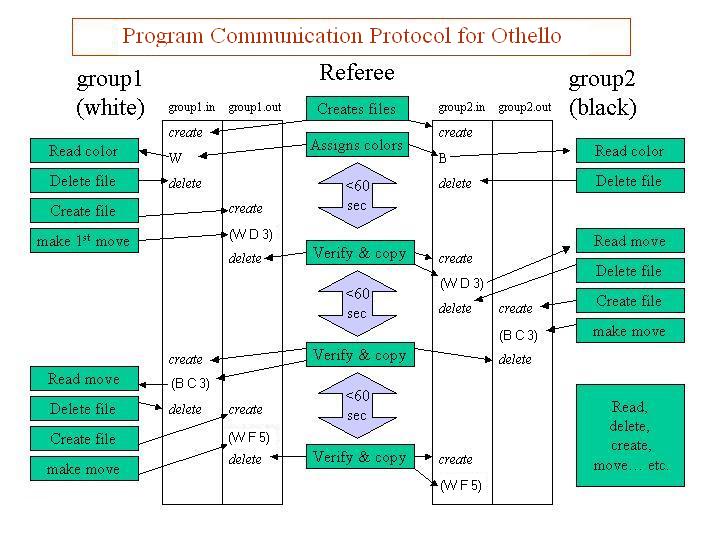
A referee program is provided. This referee program is in charge of deciding which program goes first, giving each program's turn to the other program, displaying the board configuration, detecting illegal moves, and enforcing time limits.

Here are some programs for download:

• Referee.c code by Yakov Kronrod
• Referee's executable Ref (download to a file) by Yakov Kronrod
• Sample timing code in C By Chris Shoemaker
• g1.c and g2.c to play against a human user. By Greg Milette (?)

Specifically, the referee program will be in charge of:

1. Assigning which program goes first, as described above.
2. Displaying the board configuration after each move.
3. Giving turns to each of the playing programs. By creating the file groupname.in, the referee program is giving the turn to groupname.
4. Timing each of the players. It starts measuring the time for groupname's move just after creating groupname.in.  If a program exceeds its time limit, the referee program will stop the game, announcing that the offending program has lost. (Note that a program should not time its opponent.)
5. Detecting invalid moves. If the referee program finds an invalid move, it will stop the game, announcing that the offending program has lost.
6. Ending the game when all positions on the board are occupied, announcing the winner.

TOURNAMENT

1. ALL groups who want to participate in the tournament must submit the tournament version of their code via turnin with project name 'tournament' (even if you already submitted working code).
2. 'tournament' submissions will close Sunday at noon (12:00) exactly.
3. Your program must not consume computing resources during your opponent's turn.  In this spirit, when it is your opponent's turn, your program should simply wait for your opponent's move.  Your program may check for the existence of the input file, at most, every 100 ms.  To do this, your process must block.  In C, this will probably mean some use of ualarm() and pause().  In Java, Thread.sleep() will do the trick.  In C++, maybe there are some convenient functions in <pthread_alloc>.  Whatever you do, you MAY NOT simply "burn time" by counting in some tight loop in between file checks.  Your process must block.
4. Both players will be executed on the same machine, and may not spawn processes on any other machine.
5. Time and Date: Sunday, Feb. 24th, 3 pm  
6. Place: CS Annex 
7. Points:  Your group can earn bonus points.
   • Successfully completing at least one game will give you 5 bonus points
   • For each game after that: (win = 2pts, draw = 1pt, loss = 0)
   • These bonus points will be added to your project #3 score.
   • If the bonus point scheme changes, it will only be in the positive direction.
8. Tournament structure
   • The tournament structure will be determined when we know how many groups will participate, but every group is guaranteed at least 3 games.
   • The more games your program wins, the more games your program will play.
   • Unless one of the finalist teams object, championship game will hopefully be held in class.
9. Groups
   • Please email us (cs4341_ta@cs.wpi.edu) with any additions, deletions, or name changes of group members or groups from previous projects.

REPORT SUBMISSION AND DUE DATE

Along with your code, you must also submit code documentation.  It must follow the Departmental Documentation Standard (see http://www.cs.wpi.edu/Help/documentation-standard.html).  Project 3 is due on February 17, 2002 at 9 pm.  One (and only one) member of your group must submit the following files using the turnin program:

• Documentation

1. the names of the members of your group
2. instructions on compiling and running your program
3. the static evaluation your program uses,
4. the heuristics employed,
5. strategy used for minimax and alpha beta pruning,
6. results:
   • describe which tests you ran to try out your program. Did you program play against human players? Did you program play against other programs? How did your program do during those games?
   • describe the strengths and the weaknesses of your program.
7. a discussion of why the evaluation function and the heuristic are good choices.

Finding a good static evaluation function and a good heuristic depends heavily on the experience you have with the game. I recommend you start playing the game and getting the flavor of what a good Othello strategy is. Also, research the strategies that other people have used for this and other games. Lots of information can be found in the references listed in your syllabus, the web, and magazine articles.

• Program.  
  1. The source code for your program
  2. See more information about the turnin command on http://cs.wpi.edu/Help/turnin.html

• Any auxillary files that your program requires, such as a script to run a language interpreter.

OTHER RESOURCES

• Othello (Reversi): (just some of the multiple related sites are included below)
  • Collection of Othello Data Analysis http://www.andreazinno.it/analysis.html
  • Collection of Advanced Articles http://www.io.com/~rgatliff/othello/bib3.html
  • Bluez Othello Links, (The JACKPOT page) http://bluez2000.tripod.com/OthelloLinks.html
  • Sample Online Game http://www.posi.net/software/othello/
  • MiniMax wiht AB Pruning Explanation http://yoda.cis.temple.edu:8080/UGAIWWW/lectures95/search/alpha-beta.html
  • Detailed Othello Rules and Setup http://www.centralconnector.com/GAMES/othello.html
  • Another Online Othello Demo http://www.swanlake.com/java/othello2.html
  • Online Othello with Ratings http://www.vogclub.com/game.phtml?sid=5
  • AAAI's Othello http://www.aaai.org/Pathfinder/html/othello.html

GRADING CRITERIA:

 35 points minimax implementation 
 15 points alpha-beta pruning
 15 points heuristic evaluation function, i.e. function
           that assigns a number to any intermediate board
           configuration.
 15 points heuristic strategy to avoid expanding the whole
           minimax tree so that a move is produced within
           the time limit.
 10 points playing "reasonably well" - showing evidence
           of good offensive and defensive behavior.
 10 points interacting well with referee + good documentation
----------
100 points

+ Extra points for using machine learning (decision trees,
   neural networks, genetic algorithms, etc.) to make your
   system better at playing Othello

+ Extra points for good performance in the tournament

SUMMARY OF HELP SESSIONS:(By Yakov Kronrod)

Project #3 Helpsession Review

1. Dynamics of the Game
	-make sure you play it yourself to get an idea of strategies
	-read up on existing strategies for good hints for heuristics

2. Basic Structure of an Othello Player
   a-read groupname.in to find out your color
   b-delete groupname.in
   c-BLACK will wait until the group2name.in has a move in it
    -WHITE will chose the first move, write it to group1name.out, and 
     also wait until group1name.in has a move in it

(NOTE: At this point the two players behave the same.)

 while(game is not over)
 {
   d-no processing until groupname.in exists with a move in it
   e-read in the move from groupname.in, validate it, and 
     update your board
   f-chose the next move according to MinMax with A-B Pruning
   g-write your move to groupname.out within time limit
 }

3. List of Preliminary Details (not the juicy stuff)

-you must make sure opponent move is valid.  If it is not, 
 your program should print this out to the screen and announce 
 itself the victor.
-you MUST delete groupname.in after reading it
-you have to check who won if the board is filled up (do not 
 depend on the referee)
-REMEMBER, the referee is for the tournament.  Your program is 
 responsible for the same error checking that the referee performs.
-see the referee and email sent out about timing in C.

4. Choosing the next move

There are a lot of things that can be said about choosing the 
next move.  In one regard, this is the key to this project, the 
rest is just a framework.  Of course, you will need to use the 
MinMax algorithm here with alpha-beta pruning.  The first step 
is figuring out what information you need at each node in the tree.  
 1. The board configuration
 2. the level (min/max) in the tree
 3. the alpha and beta values
 4. perhaps a list of legal moves for children nodes

With this in hand, there are several ways to go about constructing 
the tree and evaluating for the next move.  I will provide here an 
overview of what I consider an effective approach.  This method is 
similar to iterative deepening search.  Basically, you want to 
evaluate the legal-move tree to a certain depth initially, and 
chose an 'okay' move.  Then, as long as there is time available, 
you search deeper and deeper in the tree, incrementing 1 or 2 levels 
each time, updating the 'okay' move.  Once time runs out, or close to 
doing so, you write the best move you have found so far to the 
groupname.out file.  As for the implementation of the actual 
algorithm, I can throw around some ideas.
 1. You can either make copies of the board for every single 
    node and actually keep them there in memory (this could get 
    large), or you could find some backtracking scheme to avoid 
   the extra memory usage.  
 2. In Java or C++, creating a separate class for the board is 
    probably a good idea.  That way you can give it functions 
    that will make your code look clean and easy to debug.
 3. write separate functions for things such as evaluating a single 
    board, finding the legal moves given a board configuration and 
    color, checking the legality of a single move, reading and 
    writing to the .in and .out files, etc...

There are many issues that can arise and many questions that might 
be trivial to some and impossible to others.  Please use the email 
list wisely and communicate.  There are many areas of this project 
where your classmates could be your best resource.

GRADUATE CREDIT PROBLEM:

• No graduate part required this time. Just do your best job in getting the best playing system you can.