
Search method: Branch and BoundAlthough it is an informed search it only uses cost and not heuristic information. It is also guaranteed to find an optimal solution.
Search method: Depth FirstIt is not an informed search, and because the space is finite it is guaranteed to find a solution, if there is one. Depth 1st also only saves one path at a time and therefore meets the space requirements.
Search method: A*A* uses cost and heuristic, it's guaranteed to find optimal paths, and its time performance is optimal among search algorithms that find optimal paths.
Search method: Breadth FirstWill find the most shallow solution because it goes level by level. It requires less time then Iterative Deepening because it does not have to rebuild the tree.
(If you answer was Iterative Deepening you should have lost 1 point.)
Search method: Iterative DeepeningThis method allows you to only search down one path at a time while gradually increasing the depth of the search space. This way you will find the shallower solution with limited space.
(If your answer was Depth-Limited you lost 2 points because you do not know the depth. If your answer was Breadth First you also lost 2 points because of violating the memory requirement.)
Search method: Hill ClimbingHill Climbing narrows the search area to follow one path at a time through the search space. It does not find an optimal solution but it will find a good solution if one exists, given that the search space is finite.
(If your answer was Beam Search you lost 2 points because Beam Search stores more that one path at the time. Also, Beam Search is not guaranteed to find a solution. If your answer was Greedy you lost 2 points because you violated the space requirement. For Depth First you lost 2 points for not using the heuristic information that was given, preventing the search from being fast. For Iterative Deepening you lost 3 points because you did not use the heuristic information and for not going as fast as possible through the search space.)

!C: !kills( curiosity, tuna ) A4: kills( jack, tuna ) || kills( curiosity, tuna )
A7: kills( jack, tuna) A3: !animal-lover( w ) || !animal( s ) || !kills ( w, s )
w <- jack s <- tuna A8: !animal-lover( jack ) || !animal( tuna ) A6: !cat( u ) || animal( u )
u <-tuna A9: !animal-lover( jack) || !cat( tuna ) A5: cat( tuna )
A10: !animal-lover( jack ) A3: !Dog( y ) || !Owns( x, y ) || animal-lover( x )
A11: !Dog( y ) || !Owns( jack, y) A1.2: Owns( jack, Spot )
A12: !Dog( Spot ) A1.1: Dog( Spot )
A13:Success! Hence Curiosity Killed the Cat!!!
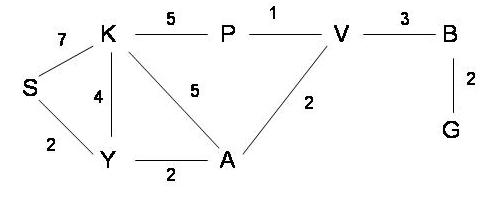
Assume also that the ESTIMATED
distances to the goal are given by the following table:
| Node: | S | K | Y | A | P | V | B | G | |||||||||
| Estimated Distance to G: | 10 | 4 | 8 | 2 | 4 | 4 | 2 | 0 |
For EACH of the following search methods list the nodes in the order in which they are EXPANDED by the search method while looking for a solution. Also, show the search tree as it is constructed by the search method. When everything else is equal, order the nodes in alphabetical order.
List of expanded nodes: S Y A K V P B G
Search Tree:
/ \
/ \
K-7 Y-2
X / \
/ \
A-4 K-6
/ | | \
/ | | \
K-9 V-6 A-11 P-11
X / \ X X
/ \
B-9 P-7
| |
| |
G-11 K-12
X
List of expanded nodes: S Y A K V B G
Search Tree:
S
/ \
/ \
K-11 Y-10
/ \
/ \
A-6 K-10
/ | | \
/ | | \
K-13 V-10 A-13 P-15
/ \
/ \
B-11 P-11
|
|
G-11
List of expanded nodes: S K A P V B G or S K A P V A B G
Search Tree(s):
S . S
/ \ . / \
/ \ . / \
K-4 Y-8 . K-4 Y-8
/ | \ . / | \
/ | \ . / | \
A-2 Y-8 P-4 . A-2 Y-8 P-4
/ | | . / | |
/ | | . / | |
Y-8 V-4 V-4 . Y-8 V-4 V-4
/ \ . / \
/ \ . / \
P-4 B-2 . A-2 B-2
| . | |
G-0 . Y-8 G-0
List of expanded nodes: S K A V B G
Search Tree:
S
/ \
/ \
K-4 Y-8
/ | \
/ | \
A-2 Y-8 P-4
/ |
/ |
/ \
/ \
P-4 B-2
|
|
G-0
A plan is a (partially) ordered collection of operators that, when applied in the order specified, tranform the initial state into the goal state.
(1) A plan is constructed using "backward chaining"
starting from the goal state and finding operators
whose postconditions match the assertions in the
goal state, and then the process is applied recursively
to satisfy the preconditions of those operators.
(2) An operator is introduced when there is an assertion
in the goal state or a precondition in any of the
operators currently in the plan that is still not
satified by other operators in the plan or the assertions
in the initial state. If there are
several operators that can be introduced to satisfy
such assertion or precondition, then those operators
are explored in a depth-1st manner (with backtracking).
(3) When the postcondition of an operator 1 in the plan
matches/satisfies the precondition of another operator 2
in the plan, we say that operator 1 "establishes"
operator 2. A "threatening" situation is present when
the postcondition of a third operator in the plan
invalidates the precondition of operator 2 that operator
1 has established.
A way to resolve this conflict is to add time constraints
to the plan, requiring that operators 1 and 2 be executed
before operator 3, or that operator 3 be executed before
operators 1 and 2. If both options are impossible to
satisfy, then the current branch of the search fails and
the whole process backtracks.
(4) The search for a plan ends successfully when all the
assertions in the goal state as well as all preconditions
of the operators in the plan are satisfied. The search for
a plan ends unsuccessfully when the search has backtracked
to the end and there are no more ways to combine the operators
to satisfy all conditions.