


This puzzle consists in finding a substitution of the letters F, O, R, T, Y, E, N, S, I, X by digits such that when each of these letters is replaced by the corresponding digit, the following sum is still arithmetically correct.
FORTY
+ TEN
+ TEN
-----
SIXTY
This puzzle has solutions. One of them is
F = 2, O = 9, R = 7, T = 8, Y = 6, E = 5, N = 0, S = 3, I = 1, X = 4
since:
29786
+ 850
+ 850
-----
31486
is arithmetically correct. Solutions to the puzzle should not repeat digits.
Your mission is to:
N and E both can take each one of two values 0 or 5. But since in the tens digit addition we need T + 2E + (carry over from units digit) = T or (10+T) hence N = 0. It follows that E = 5. Further in the thousands digit addition we have O + (carryover from hundreds place) = 10 + I. Since N = 0 hence I = 1. It follows that 0 = 9. Using this knowledge helps us to develop an informed generator. The generator is complete if we test and exhaust all possible permutations of values for the alphabets that satisfy the contraints mentioned above.
The code presented below implements a complete, informed generator. Each combination generated is tested on the fly instead of storing the combinations. The generator is non-redundant as it produces all the possible combinations in a proper sequence thus making sure that no combination is generated twice.
The code is as follows.
#include"stdio.h"
#include"math.h"
// By nature of the problem some variables can have only selected values.
// N = 0; E = 5; O = 9; I = 1;
// Using this in the generator makes it informed.
int N = 0;
int E = 5;
int O = 9;
int I = 1;
int F, R, T, Y, S, X;
main()
{
generate();
}
generate()
{
for(F=2;F<=8;F++) {
if (F==E) F++;
for(R=2;R<=8;R++) {
if ((R==F)||(R==E)) R++;
if ((R==F)||(R==E)) R++;
if (R>8) continue;
for(T=2;T<=8;T++) {
if ((T==F)||(T==R)||(T==E)) T++;
if ((T==F)||(T==R)||(T==E)) T++;
if ((T==F)||(T==R)||(T==E)) T++;
if (T>8) continue;
for(Y=2;Y<=8;Y++) {
if ((Y==F)||(Y==R)||(Y==T)||(Y==E)) Y++;
if ((Y==F)||(Y==R)||(Y==T)||(Y==E)) Y++;
if (Y>8) continue;
for(S=2;S<=8;S++) {
if ((S==F)||(S==R)||(S==T)||(S==Y)||(S==E)) S++;
if ((S==F)||(S==R)||(S==T)||(S==Y)||(S==E)) S++;
if ((S==F)||(S==R)||(S==T)||(S==Y)||(S==E)) S++;
if ((S==F)||(S==R)||(S==T)||(S==Y)||(S==E)) S++;
if ((S==F)||(S==R)||(S==T)||(S==Y)||(S==E)) S++;
if (S>8) continue;
for(X=2;X<=8;X++) {
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if ((X==F)||(X==R)||(X==T)||(X==Y)||(X==E)||(X==S)) X++;
if (X>8) continue;
test();
}
}
}
}
}
}
}
test()
{
int FORTY, TEN, SIXTY,RHS;
FORTY = (F*10000+O*1000+R*100+T*10+Y);
TEN = (T*100+E*10+N);
SIXTY = (S*10000+I*1000+X*100+T*10+Y);
RHS = FORTY + TEN + TEN;
if (SIXTY == RHS)
printf("FORTY - %d\nTEN - %d\nSIXTY - %d\n\n", FORTY,TEN,SIXTY);
}
The only solution generated is -
FORTY - 29786
TEN - 850
SIXTY - 31486
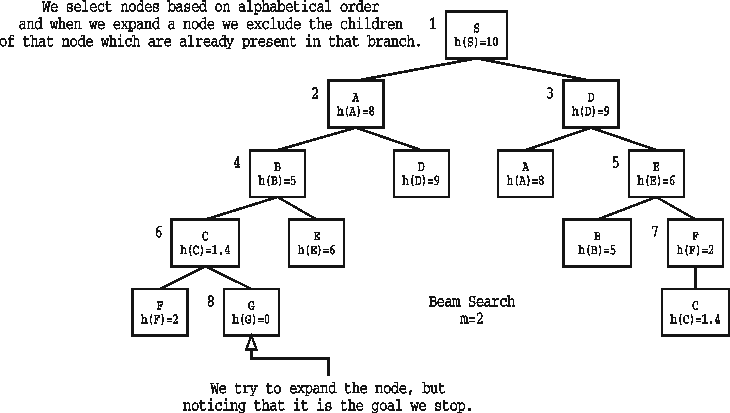
| FROM | TO | ESTIMATED DISTANCE |
| S | G | 10 |
| A | G | 8 |
| B | G | 5 |
| C | G | 1.4 |
| D | G | 9 |
| E | G | 6 |
| F | G | 2 |
| G | G | 0 |
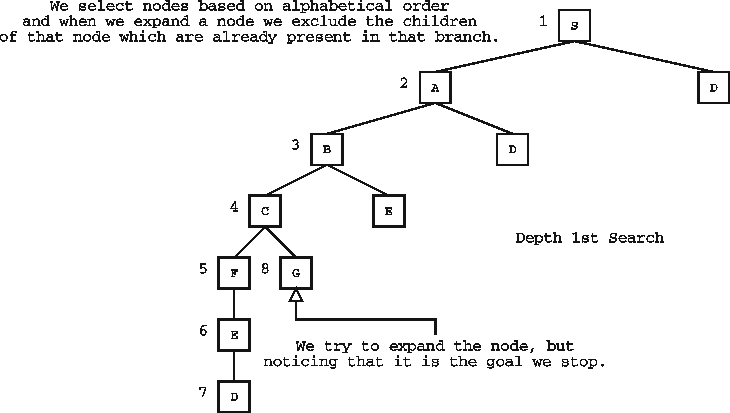
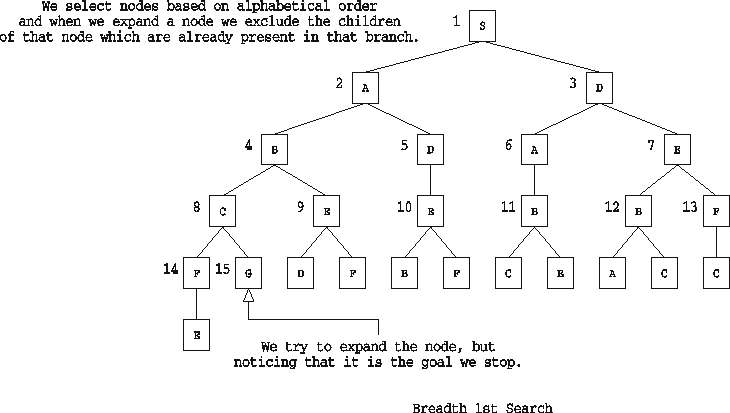
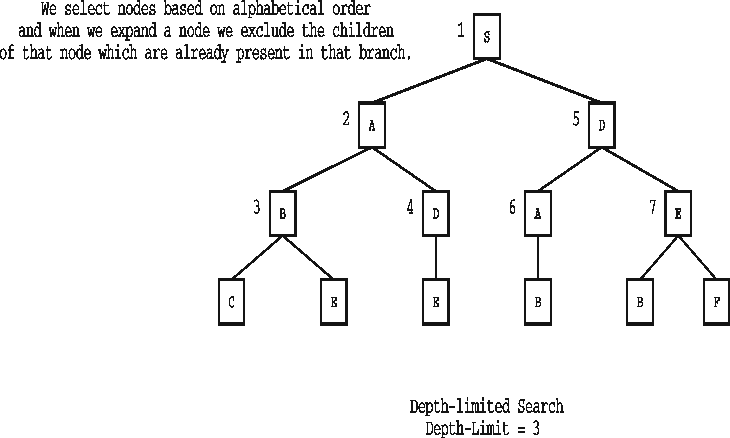
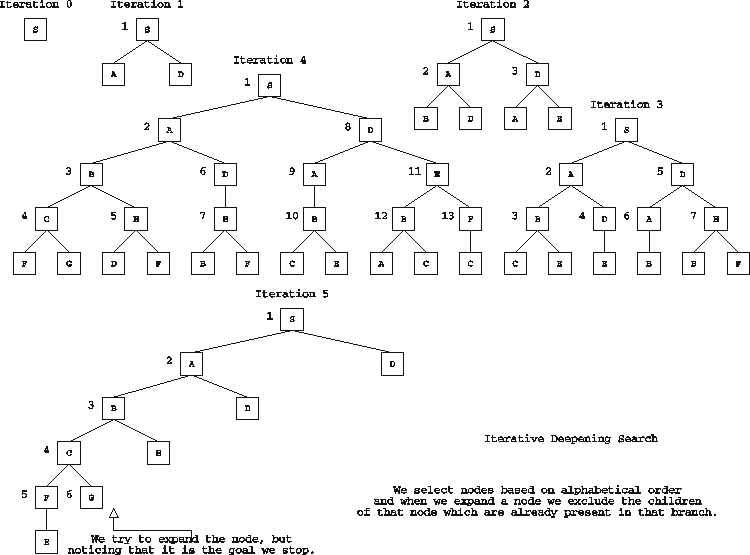
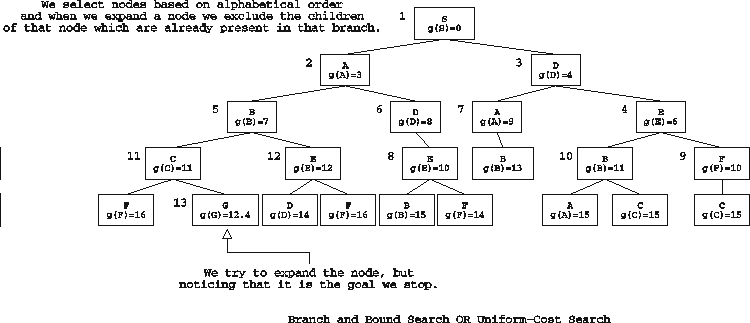
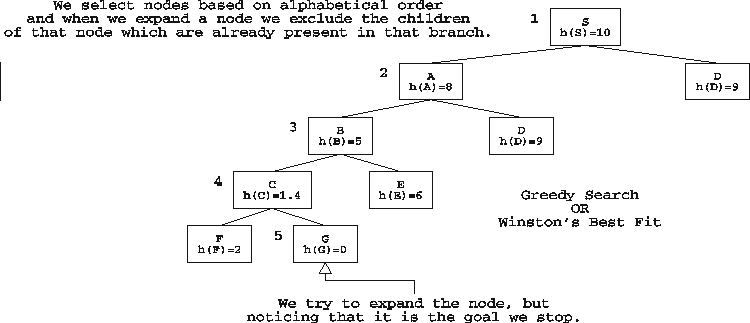
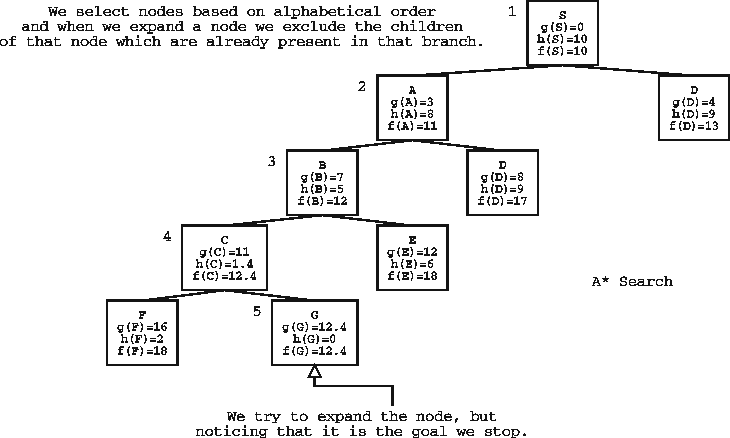
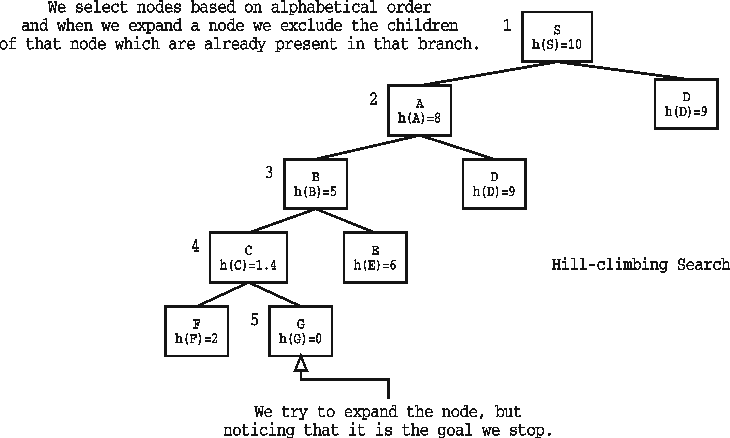
TREE 1
S
10 / \ 20
G B
| -100
G
Clearly the optimal path from S to G is S->B->G with total cost -80.
However, branch-and-bound would go over the whole process below:
1. Add S to the queue: Queue =
[S]
2. Expand S:
Queue = [G: g(G)=10, B: g(B)=20]
3. Expand G:
Goal!
So the path we found s->G is not the optimal path.
TREE 2
S
10 / \ -10
h=0 G B0 h=10
| -10
B1 h=10
| -10
B2 h=10
| -10
B3 h=10
... (the branch continues like this infinitely without reaching G)
Notice that h should be an underestimate and
Bn is an infinite path not leading to G.
From start state S, we would go over the process
below:
1. Add S to the queue: Queue =
[S]
2. Expand S:
Queue = [B0: f(B0)=0, G: f(G)=10]
3. Expand B0:
Queue = [B1: f(B1)=0, G: f(G)=10]
2. Expand B1:
Queue = [B2: f(B2)=0, G: f(G)=10]
3. Expand B2:
Queue = [B3: f(B3)=0, G: f(G)=10]
...
So we will go forever and never find a solution.