Problem I. Asymptotic Growth Rates (20 points)

• Remember that your proof must be general: it should apply to any positive functions f(n), g(n), and h(n) that satisfy the stated assumptions.
• Remember that your proof needs to be rigorous. It is not enough to give the intuition underlying the property to be proved. You need to use the definition of a function being big O ("order") of another function, and specify the necessary constants c's and n₀'s.

---

Solution:

In order to show that f(n)+g(n) = O(h(n)), we need to find constants k and n₀ such that for all n ≥ n₀, f(n)+g(n) ≤ kh(n). Since f(n) = O(h(n)) and g(n) = O(h(n)) then by definition:

• ∃ k₁ ∃ n₁ ∀ n ≥ n₁, f(n) ≤ k₁h(n).
• ∃ k₂ ∃ n₂ ∀ n ≥ n₂, g(n) ≤ k₂h(n).

Take k = k₁ + k₂, and n₀= max(n₁,n₂). Then
f(n)+g(n) ≤ k₁h(n) + k₂h(n) = (k₁ + k₂)h(n) = kh(n), for all n ≥ n₀.
Hence f(n)+g(n) = O(h(n)).

---

Problem II. Asymptotic Growth Rates (15 points)

---

Solution:

Remember that 2²ⁿ = 2ⁿ⁺ⁿ = 2ⁿ*2ⁿ. Hence:
lim_n→inf(f(n)/g(n)) = lim_n→inf(2²ⁿ/2ⁿ) = lim_n→inf(2ⁿ*2ⁿ/2ⁿ) = lim_n→inf(2ⁿ) = infinity.
Therefore, by the theorem stated in class, f(n) = Ω(g(n)).

---

Problem III. Analysis of Algorithms (45 points + 10 extra credit points)

Input:

• n: The number of men (1,...,n) = number of women (1,...,n)
• A 2-dimensional array: InverseMenPrefer[m,w] with 1 ≤ m,w ≤n. InverseMenPrefer[m,w] = i if woman w is the i^th preferred woman on man m's preference list (1st being the most preferred one).
• A 2-dimensional array: InverseWomenPrefer[w,m] with 1 ≤ w,m ≤n. InverseWomenPrefer[w,m] = j if m is the j^th preferred man on woman w's preference list (1st being the most preferred one).
• two arrays wife[m] and husband[w], with 1 ≤ m,w ≤n so that if m is matched to w then wife[m]=w and husband[w]=m.

Output:

• true, if the perfect matching given in the arrays wife and husband is stable with respect to InverseMenPrefer and InverseWomenPrefer, or
• false, otherwise, that is, if there exists an unstable pair (m,w) such that m and w prefer each other over their current spouses.

Algorithm: (See next page)

Instruction	Time taken per instruction	Number of iterations
{ stable := true . . . . . . . . . . . . . . . . . . m := 1 . . . . . . . . . . . . . . . . . . while stable AND m ≤ n do { . . . . . . . . . . . . . w := 1 . . . . . . . . . . . . . . . . . . . while stable AND w ≤ n do { . . . . . . . . . . . . . . (* we'll check below if (m,w) is an unstable pair *) if (InverseMenPrefer[m,w] < InverseMenPrefer[m,wife[m]]) AND (InverseWomenPrefer[w,m] < InverseWomenPrefer[w,husband[w]]) . . then { stable := false . . . . . . . . . . . . . } w := w + 1 . . . . . . . . . . . . . . . . . . . } m := m + 1 . . . . . . . . . . . . . . . . . . . } return(stable) . . . . . . . . . . . . . . . . . . . }	C1 C2 C3 C4 C5 C6 C7 C8 C9 C10	1 1 --------- | | | -- | | | | | | | | n | n |times |times | | | | | | | | | | -- | | --------- 1

1. (20 points) Prove that the algorithm is correct. That is, it returns true if the given perfect matching is stable, and false if it is unstable. Your proof should decisively prove each of these two cases.

   ---

   Solution:

   Let's start by noting that the "if condition"

       (InverseMenPrefer[m,w] < InverseMenPrefer[m,wife[m]])
       AND
       (InverseWomenPrefer[w,m] < InverseWomenPrefer[w,husband[w]])
   

   is true
   if and only if man m prefers woman w over his wife and w prefers m over her husband
   if and only if the pair (m,w) is unstable
   if and only if the input perfect matching is unstable.

   Let's show now that the algorithm always outputs the correct answer for the given input perfect matching:

   • If the input perfect matching is stable, then no unstable pair exists and hence the if condition is never true. Then, the variable "stable", which has been set to true at the beginning of the program, is never set to false, and the program correctly outputs "true".
   • If the input perfect matching is unstable, then there is at least one unstable pair (m,w) that makes the if condition true. Then, the variable "stable" is set to false, stopping the iterations of both while loops, and making the program correctly output "false".

   ---

2. (25 points) Analyze the runtime of your algorithm as a function of n.
   • (5 points) In the table above state how much time the execution of each instruction would take.
   • (5 points) In the table above state which instructions would be repeated and how many times they would be repeated in the worst case.
   • (5 points) Combine here the full runtime of the algorithm:

     ---

     Solution:

             T(n) = C1 + C2 + [C3 + C4 + [C5 + C6 + C7 + C8]*n + C9]*n + C10
                  = C' + [C'' + C'''*n]*n
                  = C' + C''n + C'''n2
     
             where:
                  
             C' = C1 + C2 + C10
             C'' = C3 + C4 + C9 
             C''' = C5 + C6 + C7 + C8 
             

     ---

   • (10 points) Using worst case analysis, provide an asymptotic tight bound g(n) for your T(n) function above and prove in detail that T(n) = Θ(g(n)).

     ---

     Solution:

     T(n) = C' + C''n + C'''n². Let g(n) = n².
     In order to show that T(n) = Θ(g(n)) we need to find constants k₁, k₂, and n₀ such that for all n ≥ n₀, k₁n² ≤ T(n) ≤ k₂n².
     Note that:

     • T(n) = C'+ C''n + C'''n² ≤ C'n² + C''n² + C'''n² = (C'+ C''+ C''') n² = (C'+ C''+ C''') g(n), for all n ≥ 1, and
     • T(n) = C'+ C''n + C'''n² ≥ C'''n² = C'''g(n), for all n ≥ 0.

     Hence ∃ k₁=C''' ∃ k₂=(C'+ C''+ C''') ∃ n₀=max(0,1) ∀ n ≥ n₀, k₁g(n) ≤ T(n) ≤ k₂g(n). Therefore T(n) = Θ(g(n)).

     ---

3. (10 extra credit points) Consider now best case analysis.
   • (5 points) What is the best case scenario for this algorithm? That is, given a fixed value n > 0, what property should the rest of the input satisfy so that the algorithm will run for the least possible amount of time for that input of size n?

     ---

     Solution:

     The perfect matching should be such that m₁ and w₁ (the 1st man and the 1st woman) form an unstable pair. For this particular case, the runtime of the algorithm would be:
     T(n) = C₁ + C₂ + C₃ + C₄ + C₅ + C₆ + C₇ + C₈ + C₉ + C₁₀, that constant.

     ---

   • (5 points) Provide an asymptotic lower bound h(n) for your T(n) function in this best case scenario and argue that T(n) = Ω(h(n)).

     ---

     Solution:

     T(n) = C' + C''n + C'''n². Let h(n) = 1.
     In order to show that T(n) = Ω(h(n)) we need to find constants k and n₀ such that for all n ≥ n₀, T(n) ≥ k*1.
     Note that: T(n) = C'+ C''n + C'''n² ≥ 1 for all n ≥ 1. Hence ∃ k=1 ∃ n₀=1 ∀ n ≥ n₀, T(n) ≤ k*1. Therefore T(n) = Ω(h(n)).

     ---

Problem IV. Time Complexity (20 points)

• (10 points) Consider two algorithms A and B that take time in Θ(n²) and Θ(n³), respectively, to solve the same problem. If other resources such as storage and programming time are of no concern, is it necessarily the case that algorithm A is always preferable to algorithm B? Justify your answer.

  ---

  Solution:

  
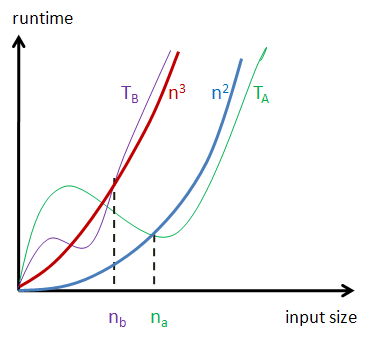
  No. Let T_A and T_B be the runtime functions of algorithms A and B, respectively. By definition, of Θ, T_A(n) has the same growth rate as n² for large enough n's (that is, for n ≥ n_A for some constant n_A ≥0), and T_B(n) has the same growth rate as n³ for large enough n's (that is, for n ≥ n_B for some constant n_B ≥0). But for some n₀ < max(n_A,n_B), it might happen that T_A(n₀) > T_B(n₀), and then B would be preferable to A on inputs of size n₀.

  ---

• (10 points) (This part is unrelated to the previous part.) Consider two algorithms C and D that take time in O(n²) and O(n³), respectively. Could there be an implementation of algorithm D that would be more efficient (in terms of computing time) than an implementation of algorithm C on each and every possible input? Justify your answer.

  ---

  Solution:

  Yes. Note that O(.) does not provide tight bounds. Take for example f(n)=n²+n and g(n)=n. It is true for these functions that f(n)=O(n²) and g(n)=O(n³). Nevertheless, g(n) ≤ f(n) for all n, and hence an implementation of algorithm D can be more efficient than an implementation of algorithm C.

  ---