CS2223 Algorithms 
Quiz 2 Solutions - B Term 2005

BY PROF. CAROLINA RUIZ 

Problem I. Greedy Algorithms (70 points)

1. (35 points) Assume that you want to make the minimum number of stops possible along the way, without running out of gas at any point. Describe in detail an efficient method by which you can determine at which gas stations you should stop.

   Solution: The following greedy approach works: Start your trip in Worcester with a full tank. Check your map to determine the farthest away gas station in your route within n miles. Stop at that gas station, fill up your tank and check your map again to determine the farthest away gas station in your route within n miles from this stop. Repeat the process until you get to San Francisco.

   ---

2. (35 points) Show that your method above produces an optimal solution (i.e., it produces the minimum number of stops possible without running out of gas).

   We include here two alternate proofs of the optimality of our greedy method above. Obviously, only one proof would suffice. Alternate Solution 1: This proof is an illustration of "the greedy algorithm stays ahead" proof method in your textbook. Note that our greedy method selected as the first stop the gas station farthest away from Worcester in your route but within n miles from Worcester. No optimal method could have selected a farther away gas station since by doing so your car would run out of gas. Hence, any other optimal method would have selected either the same gas station or another one closer to Worcester. In both cases, our greedy approach is doing no worse than any other optimal one. We can repeat the same argument for any subsequent stop. Hence, our greedy method cannot do worse than (i.e., stay behind) any optimal method and so our greedy method is optimal. Alternate Solution 2: This proof is an illustration of "an exchange argument" proof method in your textbook. Assume that our greedy method is not optimal. That is, it produces a solution that has more stops than strictly necessary. Let the sequence of stops of our greedy approach be gs1,...,gsx. Since this is not optimal, an optimal sequence of stops must constain less stops. Let os1,...,osy be such an optimal solution, where y < x. Let k be the largest index for which: gs1,...,gsk = os1,...,osk. Consider the stop k+1. We know that gsk+1 != osk+1. Since our greedy approach selected the k+1 gas station as the farthest away from gsk (= osk) but within n miles of gsk, osk+1 must be closer to gsk than gsk+1 (since if osk+1 were even farther away from gsk your car would have run out of gas, and hence the optimal solution wouldn't even be a solution!). Hence we can replace osk+1 with gsk+1 in the optimal solution, without affecting neither the size nor the correctness of the optimal solution. Now, we repeat the same exchange procedure for each subsequent stop from k+2 to y, transforming the optimal solution into os1,...,osk,gsk+1,...,gsy = gs1,...,gsk,gsk+1,...,gsy. Remember that y < x. Since the optimal solution is a solution, it means that stop osy is within n miles from San Francisco, and hence you wouldn't need to stop for gas anymore. But by our exchange argument above gsy is either equal to osy or even closer to San Francisco than osy is. Hence, our greedy algorithm would have stopped after gsy without producing the additional stops gsy+1,...,gsx. This contradicts our assumption that y < x, and this in turn contradits our original assumption that our greedy method is not optimal. Hence, our greedy method is in fact optimal as we wanted to prove.

Problem II. Priority Queues (30 points)

1. (30 points) Follow step by step the process of inserting the value 9 in the priority queue. Show with drawings how the priority queue is modified at each step and explain your answer.

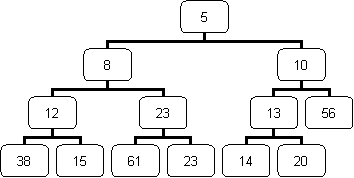
   Solution: First, the new element is added to the first (from left to right) empty spot in the leaf level of the tree (as you know, all the leaf nodes of a priority queue are always packed to the left): 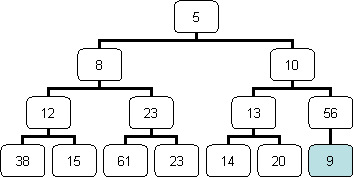Since the new element is smaller than its current parent, it is heapified-up one level (i.e., it is swapped with its current parent): The new element is still smaller than its current parent, so it is heapified-up one more level (i.e., it is swapped with its current parent): 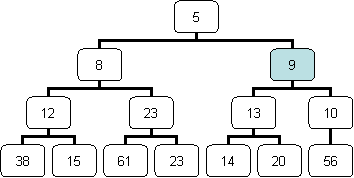The new element is now greater than or equal to its current parent, so the insertion procedure is now complete.

   ---

2. (20 extra points) Consider the insertion procedure you followed above. Let T(n) be the runtime of inserting a new element in a priority queue implemented as a heap with n elements. Find the tightest possible upper bound f(n) such that T(n)=O(f(n)). Explain your answer.

   Solution: The runtime of inserting a new element in a priority queue implemented as a heap with n elements is O(log n). It is easy to see that this is case. Since the insertion will start by adding the new element to the first free spot in the leaf level (this takes O(1)) and then heapify-ing the element up level by level while the element is smaller than its current parent. Heapifying the element one level takes O(1) as it just involves swapping the element with its current parent. In the worst case, one will need to heapify-up the element all the way to the root of the tree. Hence, the maximum number of heapify-up application will be equal to the number of levels in the tree. Since a binary tree with n elements has O(log n) (see a proof of this basic fact * below) then in the worst case, the insertion of the new element will take O(log n) time. Proof (2.12) in Section 2.5 of your textbook (p. 62) presents a similar proof of this result. * Just in case you don't remember from your discrete math course that the height of a complete binary tree that contains n elements is O(log n), I prove this result here: A complete binary tree has 1 element at level 0; 2 elements at level 1; 4 elements at level 2; and in general 2j elements at level j. Let h denote the height of the tree. Then the number of elements in the tree is: sum from j=0 to h of 2j. This is a geometric sum which is equal to (2h+1 - 1)/(2-1) = (2h+1 - 1) Since we know that the tree contains n elements, then n = (2h+1 - 1). Hence, n + 1 = 2h+1, and then log(n + 1) = h+1. From here we get that h = O(log(n+1) - 1) = O(log(n+1)) = O(log n).