Searching

Sections 2.1, 3.3 Shiflet text

We skipped ahead to hashing, which is one form of searching. Now come back to searching in general.

Definitions:

External searching: records (data) is stored in files on disk or tape. External to computer memory.

Internal searching: data is stored in memory. We will concentrate on this type of searching.

What we are searching for (or hashing on) is called the key.

Comparisons

To make a general comparison we can use the #define statement in C as a macro (substitute one string with another at compilation). We do so by specifying parameters for the statement.

We can change the type of the comparison (string, character, integer) by changing the #define statement (and nothing else).

Examples (always put parentheses around parameters to avoid precedence problems):

#define EQ(a,b) ((a) == (b))
#define LT(a,b) ((a) < (b))

#define EQ(a,b) (strcmp((a),(b)) == 0)
#define LT(a,b) (strcmp((a),(b)) < 0)

Sequential Search

Can use these macros for a sequential search for either a contiguous or linked list sequential search.

Easy to write and efficient for short lists.

Analysis of Sequential Search

Could evaluate using actual execution time, but generally characterize in terms of the number of searches (as was done for hashing):

• Best: 1

• Worst: n

• Expected:

Binary Search

Use a sorted list and divide the problem in half each time. Requires:

• a sorted list

• random access (must have data stored in an array versus a linked list)

Text: 90% of professional programmers fail to code binary search correctly after an hour!

Use two indices first and last:

• Initialize first=0 and last=cElements-1.

• Search while first<=last and not found

• The value of last-first must decrease on each iteration (to guarantee termination).

Two versions:

1. Search while first<=last and check middle value for equality each time through the loop. Compute the middle value in each iteration using integer division.

   Example: first=0, last=30 then middle=15
   Next (if target just above middle): first=16, last=30 then mid=23
   Next (if target just above middle): first=16, last=23 then mid=19
   

2. Same idea, but search until only one element left (or first and last cross over each other.

Analysis

How many comparisons are being made:

• Best: 2 (2 at each level, one for greater than and one for less than)

• Worst, Expected: need to look at comparison tree

Comparison Trees

Use circles for comparisons and branches to indicate possible outcomes. Boxes indicate completion (either success or failure).

Look at Fig 5.2 for a sequential search. The level is the number of branches from the root. The height (the highest level) of the tree is n indicating the worst case performance.

Now look at Kruse Fig 5.3 for search (use approach where only one comparison is made at each iteration). It is a 2-tree in that each node (parent) has two outcomes (children).

The number of nodes at each level t is .

The worst case and expected case are the same because we are searching for one node.

How many comparisons are expected? (n successes and n failures) =2n. So

By default always use base 2 in algorithm analysis. Average (and worst case) search time is thus comparisons.

For approach where we make two comparisons at each iteration the number of comparisons is .

Big Oh Notation

If f(n) and g(n) are functions defined for positive integers then

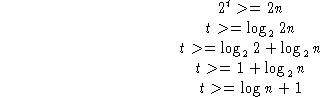
means there is a constant c such that

for sufficiently large positive integers.

In other words, the highest order term of the expression. As n gets large, the highest order term is the most important.

Characterization of worst case performance for lookup and add

Sequential search: O(n) for lookup; O(1) for adding to list

Binary search: , O(n) for adding to list

Hashing: O(n), worst case; O(1), average case for sufficiently low load factor for both lookup and adding to list.

Searching Summary

• linear--simple to program, works for either linked lists or arrays, do not need a sorted list. Inefficient for large numbers of items.

• binary search--must use arrays and maintain a sorted list, relatively fast search.

• hashing--must use arrays, use more space, but can be quick to lookup a value.