


Next: About this document
Sergio A. Alvarez
web: http://www.cs.wpi.edu/ 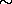 alvarez/
alvarez/
Department of Computer Science
e-mail: alvarez@cs.wpi.edu
Worcester Polytechnic Institute
phone: (508) 831-5118
Worcester, MA 01609, USA
fax: (508) 831-5776
CS 3133, A Term 1998
Final Exam Practice Problems
(also see the practice problems
for the midterm exam)
-
For each of the following pairs of languages
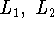 over the alphabet
over the alphabet
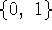 , determine whether
, determine whether 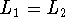 or
or 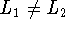 .
If
.
If 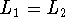 , give a regular expression for the languages.
If
, give a regular expression for the languages.
If 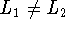 , give a string w that belongs to one of the two
languages but not the other.
, give a string w that belongs to one of the two
languages but not the other.
-
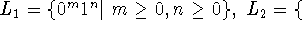 all strings not having the substring
all strings not having the substring 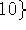 .
. -
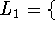 all strings that contain twice as many 1's
as 0's
all strings that contain twice as many 1's
as 0's 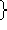 ,
,
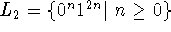 . Note that
. Note that 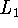 contains the
empty string.
contains the
empty string.
-
Let L be the language of all strings w over the alphabet
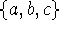 such that
such that 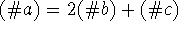 , where
, where 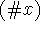 denotes the number of times that the
symbol x appears in w. For example, the string abaca is in L but aabc is not.
denotes the number of times that the
symbol x appears in w. For example, the string abaca is in L but aabc is not.
- Design an extended PDA (multiple pops and pushes allowed in a single transition)
that accepts L by final state and empty stack.
- Convert your extended PDA from part (a) into a standard PDA (only a single pop/push
allowed in each transition).
- Is L a regular language? Explain.
- Is L a context-free language? Explain.
-
- Find the language L accepted by the PDA P that has
state set
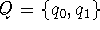 ,
accepting state set
,
accepting state set 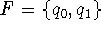 ,
input alphabet
,
input alphabet 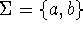 ,
stack alphabet
,
stack alphabet 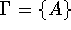 ,
and transition function
,
and transition function 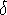 defined by
defined by
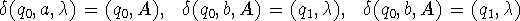
- Design a Turing machine that accepts the language L from part (a).
- Calculate the time complexity of the machine M from part (b).
-
Show that each of the following problems belongs to the class NP
by finding a deterministic polynomial time verifier. In each case,
explain what the input to the verifier is, how the verifier operates,
and why it runs in polynomial time.
- The Hamiltonian path problem: Given a graph G, determine
(yes/no answer) if there is a path in G that visits each vertex
of G exactly once.
- The graph coloring problem: Given a graph G and a natural
number k, determine (yes/no answer) if there is a coloring of
the vertices of G using k colors such that no edge of G
connects two vertices of the same color. Assume that there is
at most one edge connecting any given pair of vertices.



Next: About this document
Sergio A. Alvarez
Mon Oct 12 13:50:02 EDT 1998
![]() alvarez/
alvarez/ ![]()