


Next: About this document
Up: No Title
Previous: No Title
Sergio A. Alvarez
web: http://www.cs.wpi.edu/ 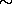 alvarez/
alvarez/
Department of Computer Science
e-mail: alvarez@cs.wpi.edu
Worcester Polytechnic Institute
phone: (508) 831-5118
Worcester, MA 01609 USA
fax: (508) 831-5776
CS 3133, A Term 1998
Midterm Exam
Read each problem carefully. Write solutions neatly in the spaces provided.
Include a brief description of your solution strategy for each problem.
-
Find a regular expression for each of the following languages over
the alphabet
 :
:
- all strings that start with (at least one) a and contain
exactly two b's.
- all strings that do not contain the substring ab.
-
Consider the context-free grammar G over
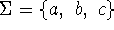 defined as follows.
defined as follows.

- Give a leftmost derivation in G for the string eabbab.
- Construct a nondeterministic finite automaton (NFA) that accepts L(G).
- Find a regular expression for the language L(G).
-
Let M be the NFA over
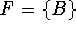 having
state set
having
state set 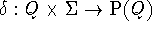 , start state A, accepting state
set
, start state A, accepting state
set 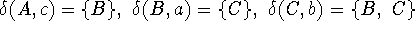 , and transition function
, and transition function
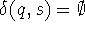 satisfying
satisfying 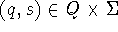 and
and 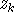 for all other pairs
for all other pairs 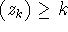 .
.
- Draw the state transition diagram of the machine M.
- Construct a deterministic finite automaton (DFA) equivalent to M.
-
In this problem L denotes the language over
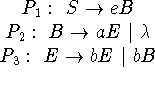 consisting of all strings that contain an equal number of a's and b's.
You will show that L is not a regular language.
consisting of all strings that contain an equal number of a's and b's.
You will show that L is not a regular language.
- For every natural number k find a string
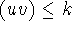 in L
of length k or greater for which pumping is guaranteed to
produce some strings that are not in L. Specifically, this means
that length
in L
of length k or greater for which pumping is guaranteed to
produce some strings that are not in L. Specifically, this means
that length 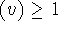 and for every decomposition of
and for every decomposition of 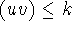 as uvw,
where the strings u, v, w satisfy length
as uvw,
where the strings u, v, w satisfy length 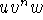 , length,
there must be some natural number n such that the pumped string is
not in L.
, length,
there must be some natural number n such that the pumped string is
not in L.
- Aiming to reach a contradiction, assume tentatively that L actually
is a regular language. Explain carefully how the pumping lemma together
with part (a) above lead to a contradiction for a certain value of k.
Explain the significance of the value of k in this context.



Next: About this document
Up: No Title
Previous: No Title
Sergio A. Alvarez
Sun Sep 20 16:24:33 EDT 1998
![]() alvarez/
alvarez/ 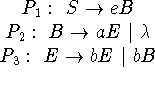 :
:
![]()
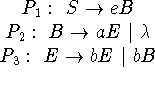 consisting of all strings that contain an equal number of a's and b's.
You will show that L is not a regular language.
consisting of all strings that contain an equal number of a's and b's.
You will show that L is not a regular language.