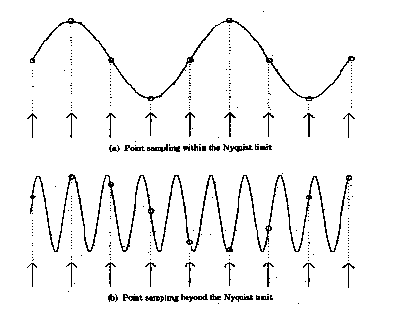

In the top sin wave, the sampling is fast enough that a reconstructed signal (the small circles) would have the same frequency as the original sin wave. In the bottom wave, with a higher frequency but the same point sampling rate, a reconstructed signal (the small circles) would appear to be a sin wave of a lower frequency, i.e., an aliased signal.
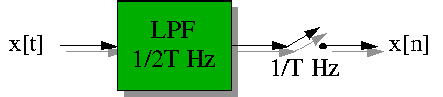
From Point Sampling Theory it turns out that to accurately reconstruct a signal, the signal must be sampled at a rate greater than or equal to two times the highest frequency contained in the signal. This is called the Nyquist Theorem and the highest frequency that can be accurately represented with a given sampling rate is called the Nyquist limit. For example, to produce a music CD-ROM the analog signal is sampled at a maximum rate of 44 Khz, therefore the highest possible audio frequency is 22khz. Any audio frequencies greater than 22Khz must be removed from the input signal or they will be aliased, i.e., appear as low frequency sounds.