These algorithms consider the image at regularly spaced sample points. They are simpler and easier to implement.
In the discrete algorithms, the generation and sampling of the image are interwined. There is no continuous image function that is sampled - an image value that is calculated at sample points. We cannot insert an antialiasing filter which operates in the continuous information domain.Another point we need to consider, is that the images which are function of spatial variables over a sampling grid.
Differences that arise in Graphics
The amplitude characteristic of most images peaks at the origin and decreases as the reciprocal of the spatial frequency. This may not be the case with graphics as it may result in high values of F(u,v) which is the transform of the two dimensional point, far away from the origin. We have to distinguish between theoretical transforms and the transforms of images on the screen. The spatial frequency of computer graphics abstractions can extend to infinity in both u & v.
Screen images are however limited in each direction by the resolution of the frame store and by the line rate and horizontal resolution of the display device.
The locus of equal spatial frequencies is a circle centered at the origin. So a perfect low pass filter is a cylinder centred at the origin. High frequencies contribute to the sharpness in the image. So removing these blurs the image. In the Fourier domain, the antialiasing operations are a tradeoff between artefact visibility and image blurring because we remove high spatial frequencies.
Thus we find that simple filtering cannot be applied in Graphics directly.
Effects caused by aliasing.
The errors caused by aliasing are called artefacts. Common aliasing artefacts include jagged profiles, disappearing or improperly rendered fine detail, and disintegrating textures.
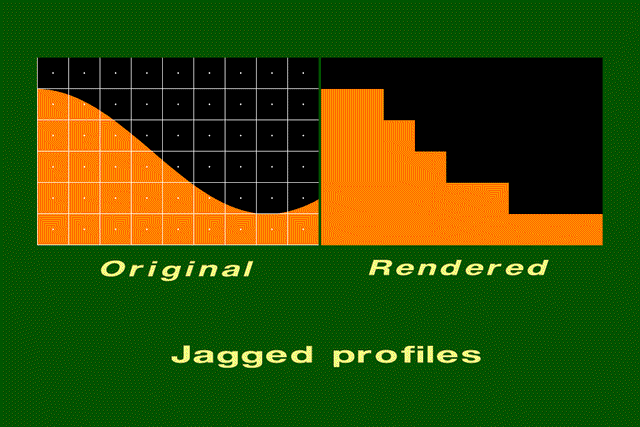
Jagged profiles.
The picture on the left shows the sampling grid superimposed on the original scene. The picture on the right is the rendered image. A jagged profile is quite evident in the rendered image. Also known as "jaggies", jagged silhouettes are probably the most familiar effect caused by aliasing. Jaggies are especially noticeable where there is a high contrast between the interior and the exterior of the silhouette.
Improperly rendered detail.
The original scene on the left shows a group of small polygons. In the rendered scene, one of the two red rectangles disappears entirely, and the other doubles in width. Two of the orange triangles disappear. Although the two yellow triangles are identical in size, one is larger than the other in the rendered image.

Disintegrating textures.
This is a checkered texture on a plane. The checkers should become smaller as the distance from the viewer increases. However, the checkers become larger or irregularly shaped when their distance from the viewer becomes too great. Simply increasing the resolution will not remove this artefact. Increasing the resolution will only move the artefact closer to the horizon.

 Back to the main screen
Back to the main screen